题目内容
(理做)已知函数f(x)=sin2x+sinxcosx+
sin(x+
)sin(x-
)
(1)当m=0时,求f(x)在区间[
,
]上的取值范围;
(2)当tanα=2时,f(α)=
,求m的值.
| m |
| 2 |
| π |
| 4 |
| π |
| 4 |
(1)当m=0时,求f(x)在区间[
| π |
| 8 |
| 3π |
| 4 |
(2)当tanα=2时,f(α)=
| 3 |
| 5 |
考点:三角函数中的恒等变换应用
专题:三角函数的求值,三角函数的图像与性质
分析:(1)首先利用恒等变换把函数关系式转化成正弦型函数,进一步利用定义域求函数的值域.
(2)先把函数变形成简单的形式,进一步利用函数的正切值,求出正弦值和余弦值,最后求出参数m的值.
(2)先把函数变形成简单的形式,进一步利用函数的正切值,求出正弦值和余弦值,最后求出参数m的值.
解答:
解:(1)当m=0时,f(x)=f(x)=sin2x+sinxcosx=
(sin2x-cos2x)+
=
sin(2x-
)+
由于x∈[
,
]
所以:2x-
∈[0,
]
sin(2x-
)∈[-
,1]
f(x)∈[0,
]
(2)由于f(x)=sin2x+sinxcosx+
sin(x+
)sin(x-
)
=
[sin2x-(1+
)cos2x]+
所以:f(α)=
[sin2α-(1+
)cos2α]+
tanα=2
所以:sin2α=
=
,cos2α=
=-
由于:f(α)=
=
[
+(1+
)]+
解得:m=-4
| 1 |
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
由于x∈[
| π |
| 8 |
| 3π |
| 4 |
所以:2x-
| π |
| 4 |
| 5π |
| 4 |
sin(2x-
| π |
| 4 |
| ||
| 2 |
f(x)∈[0,
1+
| ||
| 2 |
(2)由于f(x)=sin2x+sinxcosx+
| m |
| 2 |
| π |
| 4 |
| π |
| 4 |
=
| 1 |
| 2 |
| m |
| 2 |
| 1 |
| 2 |
所以:f(α)=
| 1 |
| 2 |
| m |
| 2 |
| 1 |
| 2 |
tanα=2
所以:sin2α=
| 2tanα |
| 1+tan2α |
| 4 |
| 5 |
| 1-tan2α |
| 1+tan2α |
| 3 |
| 5 |
由于:f(α)=
| 3 |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
| m |
| 2 |
| 1 |
| 2 |
解得:m=-4
点评:本题考查的知识要点:三角函数的恒等变换,利用正弦型函数的定义域求函数的值域,求参数的值.属于基础题型

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若
,
,
均为单位向量,且
•
=0,(
+
)•
≥
2,则|
+
+
|的最小值为( )
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
| c |
| a |
| b |
| c |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
直线x-y=0被圆x2+y2=1截得的弦长为( )
| A、2 | B、1 | C、4 | D、3 |
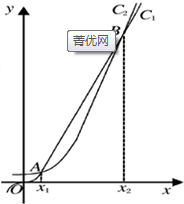 函数f(x)=2x和g(x)=x3的图象的示意图如下图所示.设两个函数的图象交于点A(x1,y1),B,2,y2)且x1<x2.
函数f(x)=2x和g(x)=x3的图象的示意图如下图所示.设两个函数的图象交于点A(x1,y1),B,2,y2)且x1<x2.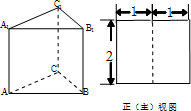 如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为( )
如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为( )