题目内容
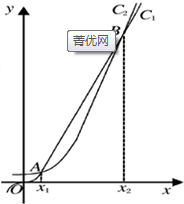 函数f(x)=2x和g(x)=x3的图象的示意图如下图所示.设两个函数的图象交于点A(x1,y1),B,2,y2)且x1<x2.
函数f(x)=2x和g(x)=x3的图象的示意图如下图所示.设两个函数的图象交于点A(x1,y1),B,2,y2)且x1<x2.(1)若x1∈[a,a+1],x2∈[b,b+1],且a,b∈{1,2,3,4,5,6,7,8,910,11,12},指出a,b的值,并说明理由;
(2)结合函数图象示意图,请把f(6),g(6),f(2007),g(2007)四个数按从小到大的顺序排列.
考点:指数函数的单调性与特殊点
专题:函数的性质及应用
分析:(1)根据指数函数、幂函数的图象特点,可得结论,令φ(x)=f(x)-g(x)=2x-x3,则x1,x2为函数φ(x)的零点,确定其所在区间,即可得出结论;
(2)从图象上可以看出,当x1<x<x2时,f(x)<g(x),当x>x2时,f(x)>g(x),即可得出结论.
(2)从图象上可以看出,当x1<x<x2时,f(x)<g(x),当x>x2时,f(x)>g(x),即可得出结论.
解答:
解:(1)C1对应的函数为g(x)=x3,C2对应的函数为f(x)=2x.a=1,b=9.理由如下:
令φ(x)=f(x)-g(x)=2x-x3,则x1,x2为函数φ(x)的零点,
由于φ(1)=1>0,φ(2)=-4<0,φ(9)=29-93<0,φ(10)=210-103>0,
则方程φ(x)=f(x)-g(x)的两个零点x1∈(1,2),x2∈(9,10),
因此整数a=1,b=9.…(9分)
(2)从图象上可以看出,当x1<x<x2时,f(x)<g(x),
∴f(6)<g(6).
当x>x2时,f(x)>g(x),∴g(2007)<f(2007),
∵g(6)<g(2007),
∴f(6)<g(6)<g(2007)<f(2007).
令φ(x)=f(x)-g(x)=2x-x3,则x1,x2为函数φ(x)的零点,
由于φ(1)=1>0,φ(2)=-4<0,φ(9)=29-93<0,φ(10)=210-103>0,
则方程φ(x)=f(x)-g(x)的两个零点x1∈(1,2),x2∈(9,10),
因此整数a=1,b=9.…(9分)
(2)从图象上可以看出,当x1<x<x2时,f(x)<g(x),
∴f(6)<g(6).
当x>x2时,f(x)>g(x),∴g(2007)<f(2007),
∵g(6)<g(2007),
∴f(6)<g(6)<g(2007)<f(2007).
点评:本题考查函数解析式的确定,考查函数的零点,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
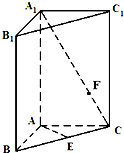 如图,三棱柱ABC-A1B1C1的底面ABC是等腰直角三角形,AB=AC=1,侧棱AA1⊥底面ABC,且AA1=2,E是BC的中点.
如图,三棱柱ABC-A1B1C1的底面ABC是等腰直角三角形,AB=AC=1,侧棱AA1⊥底面ABC,且AA1=2,E是BC的中点.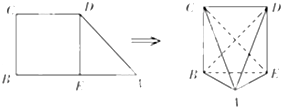 如图,梯形ABCD中,AB∥CD,∠B=∠C=90°,AB=2BC=2CD=2.E为AB中点.现将该梯形沿DE折叠.使四边形BCDE所在的平面与平面ADE垂直.
如图,梯形ABCD中,AB∥CD,∠B=∠C=90°,AB=2BC=2CD=2.E为AB中点.现将该梯形沿DE折叠.使四边形BCDE所在的平面与平面ADE垂直.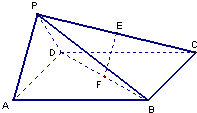 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.