题目内容
直线x-y=0被圆x2+y2=1截得的弦长为( )
| A、2 | B、1 | C、4 | D、3 |
考点:直线与圆相交的性质
专题:计算题,直线与圆
分析:圆x2+y2=1的圆心O(0,0),半径为1,直线x-y=0过圆心,可得答案.
解答:
解:圆x2+y2=1的圆心O(0,0),半径为1,直线x-y=0过圆心,
∴直线x-y=0被圆x2+y2=1截得的弦长为2,
故选:A.
∴直线x-y=0被圆x2+y2=1截得的弦长为2,
故选:A.
点评:本题考查的知识点是直线与圆的位置关系,确定直线x-y=0过圆心是解答的关键.

练习册系列答案
相关题目
若方程x2-2mx+4=0的两根满足一根大于2,一根小于2,则m的取值范围是( )
| A、(-∞,-2) |
| B、(2,+∞) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-2,+∞) |
直线y=kx+3与圆(x-2)2+(y-3)2=4相交于M、N两点,若|MN|≤2
,则k的取值范围是( )
| 3 |
A、[
| ||||||||
B、(0,
| ||||||||
C、(-∞,-
| ||||||||
D、[-
|
如果(x,y)在映射f作用下的象是(x+y,x-y),则(1,2)的象是( )
| A、(-1,3) | ||||
| B、(-3,-1) | ||||
| C、(3,-1) | ||||
D、(
|
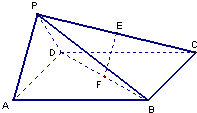 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.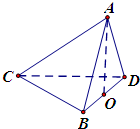 如图,四面体ABCD中,O是BD的中点,CA=CB=CD=BD=2,AB=AD=
如图,四面体ABCD中,O是BD的中点,CA=CB=CD=BD=2,AB=AD=