题目内容
在△ABC中，若sinA=2sinCcosB，则这个三角形的形状是 ．
考点：正弦定理
专题：解三角形
分析：由条件利用两角和差的正弦公式、诱导公式求得sin（C-B）=0，从而求得B=C，从而得出结论．
解答：
解：△ABC中，若sinA=2sinCcosB，则 sin（B+C）=sinBcosC+cosBsinC=2sinCcosB，
化简可得sin（C-B）=0．
再结合-π＜C-B＜π，∴C-B=0，可得B=C，故△ABC为等腰三角形，
故答案为：等腰三角形．
化简可得sin（C-B）=0．
再结合-π＜C-B＜π，∴C-B=0，可得B=C，故△ABC为等腰三角形，
故答案为：等腰三角形．
点评：本题主要考查两角和差的正弦公式、诱导公式的应用，属于基础题．
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
已知z=1+i，则(
)2=（ ）
. |
| z |
| A、2 | B、-2 | C、2i | D、-2i |
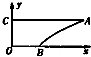如图，A（e，1），B（1，0）是曲线y=lnx图象上的两点，点A在y轴上的射影为C，O为坐标原点，则曲线梯形OBAC的面积为（ ）| A、e | B、1 | C、e-1 | D、e-2 |