题目内容
已知点F为抛物线C:y2=4x的焦点,点P为准线l上的动点,直线PF交抛物线C于A,B两点,若P的纵坐标为m(m≠0),点D为准线为l与x轴的交点,则△DAB的面积S的取值范围为( )
| A、(1,4) |
| B、(1,8) |
| C、(4,+∞) |
| D、(8,+∞) |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由抛物线C:y2=4x可得焦点F(1,0).设A(x1,y1),B(x2,y2),直线PF的方程为:y=k(x-1).与抛物线方程联立可得:k2x2-(2k2+4)x+k2=0,利用根与系数的关系可得|AB|=
.点D(-1,0)到直线AB的距离d=
.再利用S△DAB=
d|AB|即可得出.
| (1+k2)[(x1+x2)2-4x1x2] |
| |2k| | ||
|
| 1 |
| 2 |
解答:
解:由抛物线C:y2=4x可得焦点F(1,0).
设A(x1,y1),B(x2,y2),直线PF的方程为:y=k(x-1).
联立
,
化为k2x2-(2k2+4)x+k2=0,
则x1+x2=2+
,x1x2=1.
∴|AB|=
=
=
.
点D(-1,0)到直线AB的距离d=
.
∴S△DAB=
d|AB|=
×
×
=4
>4.
∴△DAB的面积S的取值范围为(4,+∞).
故选:C.
设A(x1,y1),B(x2,y2),直线PF的方程为:y=k(x-1).
联立
|
化为k2x2-(2k2+4)x+k2=0,
则x1+x2=2+
| 4 |
| k2 |
∴|AB|=
| (1+k2)[(x1+x2)2-4x1x2] |
(1+k2)[(2+
|
| 4(1+k2) |
| k2 |
点D(-1,0)到直线AB的距离d=
| |2k| | ||
|
∴S△DAB=
| 1 |
| 2 |
| 1 |
| 2 |
| |2k| | ||
|
| 4(1+k2) |
| k2 |
|
∴△DAB的面积S的取值范围为(4,+∞).
故选:C.
点评:本题考查了直线与抛物线相交问题转化为方程联立可得根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
设集合S={x|x>-2},T={x|-4≤x≤1},则(∁RS)∪T=( )
| A、{x|-2<x≤1} |
| B、{x|x≤-4} |
| C、{x|x≤1} |
| D、{x|x≥1} |
某市居民2007~2011年家庭年平均收入x(单位:万元)与年平均支出y(单位:万元)的统计资料如下表:
根据统计资料,分析下列结论正确的是( )
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 |
| 收入x | 11.5 | 12.1 | 13 | 13.4 | 15 |
| 支出Y | 6.8 | 8.8 | 9.8 | 10 | 12 |
| A、年平均收入的中位数是13,年平均收入x与年平均支出y具有正相关的相关关系 |
| B、年平均收入的中位数是13.2,年平均收入x与年平均支出y具有负相关的相关关系 |
| C、年平均收入的中位数是13,年平均收入x与年平均支出y具有负相关的相关关系 |
| D、年平均收入的中位数是13.2,年平均收入x与年平均支出y具有正相关的相关关系 |
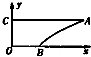 如图,A(e,1),B(1,0)是曲线y=lnx图象上的两点,点A在y轴上的射影为C,O为坐标原点,则曲线梯形OBAC的面积为( )
如图,A(e,1),B(1,0)是曲线y=lnx图象上的两点,点A在y轴上的射影为C,O为坐标原点,则曲线梯形OBAC的面积为( )| A、e | B、1 | C、e-1 | D、e-2 |
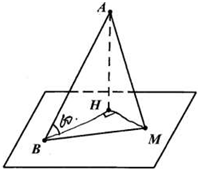 某风景区有空中景点A及平坦的地面上景点B.已知AB与地面所成角的大小为60°,点A在地面上的射影为H,如图,请在地面上选定点M,使得
某风景区有空中景点A及平坦的地面上景点B.已知AB与地面所成角的大小为60°,点A在地面上的射影为H,如图,请在地面上选定点M,使得