题目内容
已知∈[-3,2],求f(x)=
-
+1的最大值和最小值.
| 1 |
| 4x |
| 2 |
| 2x |
考点:指数型复合函数的性质及应用
专题:函数的性质及应用
分析:设t=(
)x,t∈[
,8],转化为g(t)=t2-2t+1,t∈[
,8],根据二次函数的单调性求解即可.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:设t=(
)x,t∈[
,8],
∵f(x)=
-
+1,
∴g(t)=t2-2t+1,t∈[
,8],
根据二次函数的单调性:最大值g(8)=64-16+1=49,
最小值:g(1)=0,
| 1 |
| 2 |
| 1 |
| 4 |
∵f(x)=
| 1 |
| 4x |
| 2 |
| 2x |
∴g(t)=t2-2t+1,t∈[
| 1 |
| 4 |
根据二次函数的单调性:最大值g(8)=64-16+1=49,
最小值:g(1)=0,
点评:本题考查了换元法转化为二次函数,运用单调性求解,关键是确定新变量的范围,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
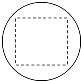 已知某一多面体内接于球构成一个组合体,如果该组合体的正视图,侧视图,俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )
已知某一多面体内接于球构成一个组合体,如果该组合体的正视图,侧视图,俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )| A、4π | B、8π |
| C、12π | D、16π |