题目内容
已知n∈N*,则[x2+(
)3]4展开式的x3系项为 .
| 1 |
| x |
考点:二项式定理的应用
专题:二项式定理
分析:利用二项展开式的通项公式求出展开式的通项,令x的指数为3,求出结果.
解答:
解:[x2+(
)3]4展开式的通项为:
(x2)4-r[(
)3]r=
x8-5r,令8-5r=3,解得r=1,
∴T2=
x3,
[x2+(
)3]4展开式的x3系项为:4.
故答案为:4.
| 1 |
| x |
| C | r 4 |
| 1 |
| x |
| C | r 4 |
∴T2=
| C | 1 4 |
[x2+(
| 1 |
| x |
故答案为:4.
点评:本题考查利用二项展开式的通项公式解决二项展开式的特定项问题.

练习册系列答案
相关题目
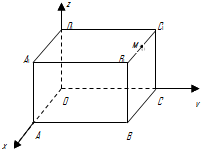 如图所示的空间直角坐标系O-xyz下,长方体OABC-D1A1B1C1中,|OA|=3,|OC|=4,|OD1|=2,则B1C1的中点M的坐标是( )
如图所示的空间直角坐标系O-xyz下,长方体OABC-D1A1B1C1中,|OA|=3,|OC|=4,|OD1|=2,则B1C1的中点M的坐标是( )A、(
| ||
| B、(3,2,2) | ||
| C、(3,4,1) | ||
D、(
|
已知f(x)=2+log3x,x∈[
,9],则f(x)的最小值为( )
| 1 |
| 81 |
| A、-2 | B、-3 | C、-4 | D、0 |