题目内容
已知向量
=（m，cos2x），
=（sin2x，n），函数f（x）=
•
，且y=f（x）的图象过点（
，
）和点（
，-2）．
（Ⅰ）求m，n的值；
（Ⅱ）将y=f（x）的图象向左平移φ（0＜φ＜π）个单位后得到函数y=g（x）的图象，若y=g（x）图象上的最高点到点（0，3）的距离的最小值为1，求y=g（x）的单调递增区间．
| a |
| b |
| a |
| b |
| π |
| 12 |
| 3 |
| 2π |
| 3 |
（Ⅰ）求m，n的值；
（Ⅱ）将y=f（x）的图象向左平移φ（0＜φ＜π）个单位后得到函数y=g（x）的图象，若y=g（x）图象上的最高点到点（0，3）的距离的最小值为1，求y=g（x）的单调递增区间．
考点：平面向量数量积的运算,正弦函数的单调性,函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质,平面向量及应用
分析：（Ⅰ）由题意可得 函数f（x）=msin2x+ncos2x，再由y=f（x）的图象过点（
，
）和点（
，-2），解方程组求得m、n的值．
（Ⅱ）由（Ⅰ）可得f（x）=2sin（2x+
），根据函数y=Asin（ωx+φ）的图象变换规律求得g（x）=2sin（2x+2φ+
）的图象，再由函数g（x）的一个最高点在y轴上，求得φ=
，可得g（x）=2cos2x．令2kπ-π≤2x≤2kπ，k∈Z，求得x的范围，可得g（x）的增区间．
| π |
| 12 |
| 3 |
| 2π |
| 3 |
（Ⅱ）由（Ⅰ）可得f（x）=2sin（2x+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
解答：
解：（Ⅰ）由题意可得 函数f（x）=
•
=msin2x+ncos2x，
再由y=f（x）的图象过点（
，
）和点（
，-2），可得
．
解得 m=
，n=1．
（Ⅱ）由（Ⅰ）可得f（x）=
sin2x+cos2x=2（
sin2x+
cos2x）=2sin（2x+
）．
将y=f（x）的图象向左平移φ（0＜φ＜π）个单位后，
得到函数g（x）=2sin[2（x+φ）+
]=2sin（2x+2φ+
）的图象，显然函数g（x）最高点的纵坐标为2．
y=g（x）图象上各最高点到点（0，3）的距离的最小值为1，
故函数g（x）的一个最高点在y轴上，
∴2φ+
=2kπ+
，k∈Z，结合0＜φ＜π，可得φ=
，
故g（x）=2sin（2x+
）=2cos2x．
令2kπ-π≤2x≤2kπ，k∈Z，求得 kπ-
≤x≤kπ，
故y=g（x）的单调递增区间是[kπ-
，kπ]，k∈Z．
| a |
| b |
再由y=f（x）的图象过点（
| π |
| 12 |
| 3 |
| 2π |
| 3 |
|
解得 m=
| 3 |
（Ⅱ）由（Ⅰ）可得f（x）=
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
将y=f（x）的图象向左平移φ（0＜φ＜π）个单位后，
得到函数g（x）=2sin[2（x+φ）+
| π |
| 6 |
| π |
| 6 |
y=g（x）图象上各最高点到点（0，3）的距离的最小值为1，
故函数g（x）的一个最高点在y轴上，
∴2φ+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
故g（x）=2sin（2x+
| π |
| 2 |
令2kπ-π≤2x≤2kπ，k∈Z，求得 kπ-
| π |
| 2 |
故y=g（x）的单调递增区间是[kπ-
| π |
| 2 |
点评：本题主要考查两个向量的数量积公式，三角恒等变换，函数y=Asin（ωx+φ）的图象变换规律，余弦函数的单调性，体现了转化的数学思想，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
i为虚数单位，（
）2=（ ）
| 1-i |
| 1+i |
| A、-1 | B、1 | C、-i | D、i |
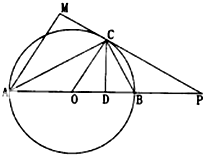如图，已知AB是⊙O的直径，C为⊙O上一点，以C为切点的切线交AB的延长线于点P，AM⊥CP，垂足为M，CD⊥AB，垂足为D．
高三（2）班在一次数学考试中，对甲、乙两组各12名同学的成绩进行统计分析，两组成绩的茎叶图如图所示，成绩不少于90分为及格，现从两组成绩中按分层抽样抽取一个容量为6的样本，则不及格分数应抽