题目内容
9．
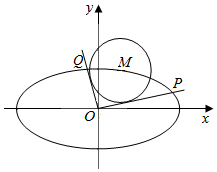如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），离心率e=$\frac{\sqrt{2}}{2}$，M（x0，y0）是椭圆上的任一点，从原点O向圆M：（x-x0）2+（y-y0）2=2作两条切线，分别交椭圆于点P，Q．（Ⅰ）若过点（0，-b），（a，0）的直线与原点的距离为$\sqrt{2}$，求椭圆方程；
（Ⅱ）在（Ⅰ）的条件下，若直线OP，OQ的斜率存在，并记为k1，k2．试问k1k2是否为定值？若是，求出该值；若不是，说明理由．
分析 （Ⅰ）运用离心率公式，以及点到直线的距离公式，结合椭圆基本量的关系，解方程可得a，b，进而得到椭圆方程；
（Ⅱ）由直线OP：y=k1x，OQ：y=k2x，与圆M相切，运用直线和圆相切的条件：d=r，化简整理，结合二次方程的韦达定理，再由点满足椭圆方程，计算即可得到定值．
解答 解：（Ⅰ）因为离心率$e=\frac{{\sqrt{2}}}{2}$，所以$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$，而c2=a2-b2，
所以$\frac{{{a^2}-{b^2}}}{a^2}=\frac{1}{2}$，即a2=2b2①
设经过点（0，-b），（a，0）的直线方程为$\frac{x}{a}+\frac{y}{-b}=1$，
即bx-ay-ab=0，
因为直线与原点的距离为$\sqrt{2}$，
所以$\frac{|ab|}{{\sqrt{{a^2}+{b^2}}}}=\sqrt{2}$，整理得：$\frac{{{a^2}{b^2}}}{{{a^2}+{b^2}}}=2$②
由①②得$\left\{\begin{array}{l}{a^2}=6\\{b^2}=3\end{array}\right.$，
所以椭圆的方程为$\frac{x^2}{6}+\frac{y^2}{3}=1$；
（Ⅱ）因为直线OP：y=k1x，OQ：y=k2x，与圆M相切，
由直线和圆相切的条件：d=r，可得$\frac{{|{k_1}{x_0}-{y_0}|}}{{\sqrt{1+{k_1}^2}}}=\frac{{|{k_2}{x_0}-{y_0}|}}{{\sqrt{1+{k_2}^2}}}=\sqrt{2}$，
平方整理，可得${k_1}^2（2-{x_0}^2）+2{k_1}{x_0}{y_0}+2-{y_0}^2=0$，
${k_2}^2（2-{x_0}^2）+2{k_2}{x_0}{y_0}+2-{y_0}^2=0$，
所以k1，k2是方程${k^2}（2-2{x_0}^2）+2k{x_0}{y_0}+2-{y_0}^2=0$的两个不相等的实数根，
${k_1}{k_2}=\frac{{2-{y_0}^2}}{{2-{x_0}^2}}$，
因为点R（x0，y0）在椭圆C上，所以$\frac{{{x_0}^2}}{6}+\frac{{{y_0}^2}}{3}=1$，
即${y_0}^2=3（1-\frac{{{x_0}^2}}{6}）=3-\frac{1}{2}x_0^2$，
所以${k_1}{k_2}=\frac{{2-3+\frac{1}{2}x_0^2}}{2-x_0^2}=-\frac{1}{2}$为定值．
点评 本题考查椭圆的方程的求法，注意运用椭圆的离心率公式和点到直线的距离公式，考查直线的斜率之积为定值的问题，注意运用直线和圆相切的条件：d=r，考查化简整理的运算能力，属于中档题．
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{3}{4}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |