题目内容
16.设函数f(x)=ax1nx+be(其中a,b∈R,e为自然对数的底数,e=2.71828…)曲线y=f(x)在点(e,f(e))处的切线方程为y=2x,g(x)=$\frac{2x}{{e}^{x}}$-$\frac{3}{e}$+e.(1)求a,b;
(2)证明:对任意x1,x2∈(0,+∞),f(x1)≥g(x2).
分析 (1)求出函数的导数,求得切线的斜率和切点,由切线的方程,可得a,b的方程,解得a,b;
(2)分别求出f(x)、g(x)的导数,求得单调区间和极值、最值,得到f(x)的最小值不小于g(x)的最大值,即可得证.
解答 解:(1)函数f(x)=ax1nx+be的导数为f′(x)=a(1+lnx),
可得y=f(x)在点(e,f(e))处的切线斜率为2a,
由切线方程y=2x,可得2a=2,解得a=1.
由切点(e,e+be),可得e+be=2e,解得b=1;
(2)证明:函数f(x)的导数为f′(x)=1+lnx,
当x>$\frac{1}{e}$时,f′(x)>0,f(x)递增;
当0<x<$\frac{1}{e}$时,f′(x)<0,f(x)递减.
即有x=$\frac{1}{e}$处f(x)取得最小值,且为e-$\frac{1}{e}$;
函数g(x)=$\frac{2x}{{e}^{x}}$-$\frac{3}{e}$+e的导数为g′(x)=$\frac{2(1-x)}{{e}^{x}}$,
当0<x<1时,g′(x)>0,g(x)递增;
当x>1时,g′(x)<0,g(x)递减.
可得x=1处g(x)取得最大值,且为e-$\frac{1}{e}$.
综上可得f(x)≥e-$\frac{1}{e}$≥g(x),
即有对任意x1,x2∈(0,+∞),f(x1)≥g(x2).
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查不等式恒成立问题的解法,注意运用转化思想,转化为求最值问题,考查运算能力,属于中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
6.实数a,b,c满足$\left\{\begin{array}{l}{a>0}\\{{b}^{2}=ac}\\{5b≥2(a+c)}\end{array}\right.$,则$\frac{5a+8b+4c}{a+b}$的取值范围是( )
| A. | [$\frac{5}{12}$,$\frac{11}{6}$] | B. | (-∞,$\frac{5}{12}$]∪[$\frac{11}{6}$,+∞) | C. | [$\frac{20}{3}$,$\frac{37}{3}$] | D. | (-∞,$\frac{20}{3}$]∪[$\frac{37}{3}$,+∞) |
4.双曲线的离心率e=$\sqrt{2}$,经过M(-5,3)的方程是( )
| A. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{16}$=1 | C. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{9}$=1 | D. | $\frac{{y}^{2}}{25}$-$\frac{{x}^{2}}{9}$=1 |
8.已知椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>0,b>0).双曲线C2:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的渐近线方程为x$±\sqrt{3}$y=0,则C1与C2的离心率之积为( )
| A. | $\frac{{\sqrt{15}}}{4}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{6}}}{5}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
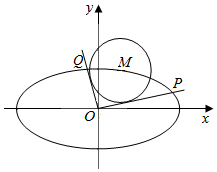 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),离心率e=$\frac{\sqrt{2}}{2}$,M(x0,y0)是椭圆上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P,Q.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),离心率e=$\frac{\sqrt{2}}{2}$,M(x0,y0)是椭圆上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P,Q.