题目内容
14.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的离心率为$\frac{1}{2}$,点F1,F2分别是椭圆C的左、右焦点,以原点为圆心,椭圆C的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切.(1)求椭圆C的方程;
(2)若过点F2的直线l与椭圆C相交于M,N两点,求使△F1MN面积最大时直线l的方程.
分析 (1)由离心率为$\frac{1}{2}$,得$\frac{c}{a}$=$\frac{1}{2}$,根据圆与直线相切可得b=$\frac{\sqrt{6}}{\sqrt{2}}$=$\sqrt{3}$,再由a2=b2+c2联立可解得a,b,即可得到椭圆方程;
(2)设直线l的方程为x=my+1,M(x1,y1),N(x2,y2),联立直线l方程与椭圆方程消掉x得y的二次方程,运用韦达定理,由S${\;}_{△MN{F}_{1}}$=$\frac{1}{2}$|F1F2|•|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$,代入韦达定理即可得关于m的函数表达式,恰当变形后,利用函数单调性求得其最大值及相应m值.
解答 解:(1)由题意得e=$\frac{c}{a}$=$\frac{1}{2}$,a2-b2=c2,
由圆x2+y2=b2与直线x-y+$\sqrt{6}$=0相切,可得
b=$\frac{\sqrt{6}}{\sqrt{2}}$=$\sqrt{3}$,解得a=2,c=1,
所以椭圆C的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)由题意可设直线l的方程为x=my+1,
设M(x1,y1),N(x2,y2),
则点M、N的坐标是方程组$\left\{\begin{array}{l}{x=my+1}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$的两组解,
消掉x得,(3m2+4)y2+6my-9=0,
所以△=36m2+36(3m2+4)>0恒成立,
y1+y2=-$\frac{6m}{3{m}^{2}+4}$,y1y2=-$\frac{9}{3{m}^{2}+4}$,
所以S${\;}_{△MN{F}_{1}}$=$\frac{1}{2}$|F1F2|•|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{\frac{36{m}^{2}}{(3{m}^{2}+4)^{2}}+\frac{36}{3{m}^{2}+4}}$=$\frac{12\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$=$\frac{12}{\frac{3{m}^{2}+4}{\sqrt{{m}^{2}+1}}}$=$\frac{12}{3\sqrt{{m}^{2}+1}+\frac{1}{\sqrt{{m}^{2}+1}}}$,
设t=$\sqrt{{m}^{2}+1}$(t≥1),由y=3t+$\frac{1}{t}$的导数3-$\frac{1}{{t}^{2}}$>0,
可得函数y在t≥1递增,即有y≥4,
S${\;}_{△MN{F}_{1}}$≤3(当且仅当m=0时取等号),
所以当m=0时,△F1MN的面积取最大值,此时直线l的方程为x=1.
点评 本题考查直线方程、椭圆方程及直线和椭圆、圆的位置关系,考查三角形面积公式,考查学生分析解决问题的能力.

| A. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{16}$=1 | C. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{9}$=1 | D. | $\frac{{y}^{2}}{25}$-$\frac{{x}^{2}}{9}$=1 |
| A. | ab-3a-b=0 | B. | ab-a-3b=0 | C. | ab-a-b=0 | D. | ab+a-b=0 |
| A. | $\sqrt{2}$+1 | B. | 2 | C. | 2$\sqrt{2}$+2 | D. | 4 |
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
| A. | 5 | B. | 16 | C. | 80 | D. | -80 |
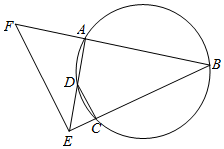 如图,A,B,C,D四点共圆,BC,AD的延长线交于点E,点F在BA的延长线上,
如图,A,B,C,D四点共圆,BC,AD的延长线交于点E,点F在BA的延长线上,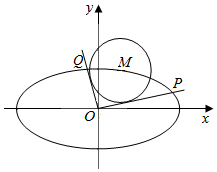 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),离心率e=$\frac{\sqrt{2}}{2}$,M(x0,y0)是椭圆上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P,Q.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),离心率e=$\frac{\sqrt{2}}{2}$,M(x0,y0)是椭圆上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P,Q.