题目内容
函数f(x)=2sin
sin(
-
)的最大值等于( )
| x |
| 2 |
| π |
| 3 |
| x |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:首先通过三角恒等变换把函数的关系式变形成正弦型函数,进一步利用正弦型函数的性质求出函数的值域.
解答:
解:f(x)=2sin
sin(
-
)
=2sin
(
cos
-
sin
)
=
sin
cos
-sin2
=
sinx-
=sin(x+
)-
当x+
=2kπ+
时,即x=2kπ+
时,函数f(x)max=
故选:A
| x |
| 2 |
| π |
| 3 |
| x |
| 2 |
=2sin
| x |
| 2 |
| ||
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
=
| 3 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
=
| ||
| 2 |
| 1-cosx |
| 2 |
=sin(x+
| π |
| 6 |
| 1 |
| 2 |
当x+
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
故选:A
点评:本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数的性质的应用,函数的值域的应用,属于基础题型.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
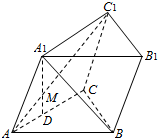 如图,已知斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=a,点A1在底面ABC上的射影恰为AC的中点D,A1D∩AC1=M,BA1⊥AC1.
如图,已知斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=a,点A1在底面ABC上的射影恰为AC的中点D,A1D∩AC1=M,BA1⊥AC1.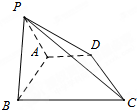 已知直角梯形ABCD中,AD∥BC,AD=AB=
已知直角梯形ABCD中,AD∥BC,AD=AB=