题目内容
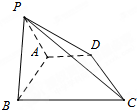 已知直角梯形ABCD中,AD∥BC,AD=AB=
已知直角梯形ABCD中,AD∥BC,AD=AB=| 1 |
| 2 |
(1)求二面角P-CD-B的余弦值;
(2)求B到平面PDC的距离.
考点:点、线、面间的距离计算,二面角的平面角及求法
专题:
分析:(1)过P作PH⊥AB,垂足为H,则PH⊥ABCD,过H作HE⊥DC交DC于E,交AD于F,证明∠PEH为二面角P-CD-B的平面角,即可求出二面角P-CD-B的余弦值;
(2)利用等体积,求B到平面PDC的距离.
(2)利用等体积,求B到平面PDC的距离.
解答:
 解:(1)过P作PH⊥AB,垂足为H,则PH⊥ABCD,过H作HE⊥DC交DC于E,交AD于F,
解:(1)过P作PH⊥AB,垂足为H,则PH⊥ABCD,过H作HE⊥DC交DC于E,交AD于F,
则∠PEH为二面角P-CD-B的平面角.
∵△EDF为等腰直角三角形,AB=2⇒AH=1
∵∠BCD=45°⇒∠ADE=45°⇒∠EFD=∠AFH=45°
∴AH=AF=1,EF=DE=
∴HE=
+
=
,PH=
∴tan∠PEH=
=
∴cos∠PEH=
…(6分)
(2)∵DC=2
,PE2=(
)2+(
)2=
,PE=
,
∴VB-PDC=
S△PDC•h=
S△PDC•PH⇒h=
…(12分)
 解:(1)过P作PH⊥AB,垂足为H,则PH⊥ABCD,过H作HE⊥DC交DC于E,交AD于F,
解:(1)过P作PH⊥AB,垂足为H,则PH⊥ABCD,过H作HE⊥DC交DC于E,交AD于F,则∠PEH为二面角P-CD-B的平面角.
∵△EDF为等腰直角三角形,AB=2⇒AH=1
∵∠BCD=45°⇒∠ADE=45°⇒∠EFD=∠AFH=45°
∴AH=AF=1,EF=DE=
| ||
| 2 |
∴HE=
| 2 |
| ||
| 2 |
3
| ||
| 2 |
| 3 |
∴tan∠PEH=
| ||||
|
| ||
| 3 |
∴cos∠PEH=
| ||
| 5 |
(2)∵DC=2
| 2 |
| 3 |
3
| ||
| 2 |
| 15 |
| 2 |
| ||
| 2 |
∴VB-PDC=
| 1 |
| 3 |
| 1 |
| 3 |
4
| ||
| 5 |
点评:本题考查二面角P-CD-B的余弦值,考查三棱锥的体积的求法,是中档题,解题时要注意空间中线线、线面、面面间的位置关系及性质的合理运用.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
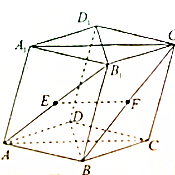 如图所示,四棱柱ABCD-A1B1C1D1中,E、F分别是AB1、BC1的中点,下列结论中,正确的是( )
如图所示,四棱柱ABCD-A1B1C1D1中,E、F分别是AB1、BC1的中点,下列结论中,正确的是( )| A、EF⊥BB1 |
| B、EF∥平面ACC1A1 |
| C、EF⊥BD |
| D、EF⊥平面BCC1B1 |
函数f(x)=2sin
sin(
-
)的最大值等于( )
| x |
| 2 |
| π |
| 3 |
| x |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
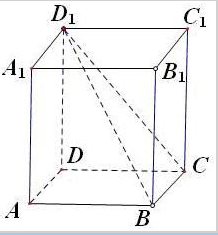 设正方体ABCD-A1B1C1D1的棱长为1,则:
设正方体ABCD-A1B1C1D1的棱长为1,则: 如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ.设直线PQ过点T(5,-2),则以PQ为底边的等腰三角形APQ个数为 ( )
如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ.设直线PQ过点T(5,-2),则以PQ为底边的等腰三角形APQ个数为 ( )