题目内容
已知椭圆
+
=1，F为右焦点，A为长轴的左端点，P点为该椭圆上的动点，则能够使
•
=0的P点的个数为（ ）
| x2 |
| 4 |
| y2 |
| 3 |
| PA |
| PF |
| A、4 | B、3 | C、2 | D、1 |
考点：椭圆的简单性质
专题：平面向量及应用,直线与圆,圆锥曲线的定义、性质与方程
分析：求出椭圆a，b，c，可得F，A的坐标，由向量垂直的条件可得P在以AF为直径的圆上，求出圆的方程，联立椭圆方程，消去y，解关于x的方程，即可得到交点个数．
解答：
解：椭圆
+
=1的a=2，b=
，c=1，
即有F（1，0），A（-2，0），
•
=0即为PA⊥PF，
即有P在以AF为直径的圆上，
则圆的方程为（x+
）2+y2=
，①
又P在椭圆上，则有
+
=1，②
由①②消去y，得x2+4x+4=0，
解得x1=x2=-2，代入可得y=0，
则只有一个交点（-2，0）．
故选D．
| x2 |
| 4 |
| y2 |
| 3 |
| 3 |
即有F（1，0），A（-2，0），
| PA |
| PF |
即有P在以AF为直径的圆上，
则圆的方程为（x+
| 1 |
| 2 |
| 9 |
| 4 |
又P在椭圆上，则有
| x2 |
| 4 |
| y2 |
| 3 |
由①②消去y，得x2+4x+4=0，
解得x1=x2=-2，代入可得y=0，
则只有一个交点（-2，0）．
故选D．
点评：本题考查椭圆的方程和性质，同时考查圆的方程的求法，联立椭圆方程和圆的方程，消去未知数，解二次方程是解题的关键．
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目
如图所示，四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是直角梯形，∠BAD=∠ABC=90°，PA=AD=2，AB=BC=1．试问在线段PA上是否存在一点M到平面PCD的距离为
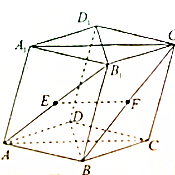如图所示，四棱柱ABCD-A1B1C1D1中，E、F分别是AB1、BC1的中点，下列结论中，正确的是（ ）| A、EF⊥BB1 |
| B、EF∥平面ACC1A1 |
| C、EF⊥BD |
| D、EF⊥平面BCC1B1 |
函数f（x）=2sin
sin（
-
）的最大值等于（ ）
| x |
| 2 |
| π |
| 3 |
| x |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
如图，已知抛物线C：y2=4x，过点A（1，2）作抛物线C的弦AP，AQ．设直线PQ过点T（5，-2），则以PQ为底边的等腰三角形APQ个数为 （ ）