题目内容
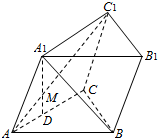 如图,已知斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=a,点A1在底面ABC上的射影恰为AC的中点D,A1D∩AC1=M,BA1⊥AC1.
如图,已知斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=a,点A1在底面ABC上的射影恰为AC的中点D,A1D∩AC1=M,BA1⊥AC1.(Ⅰ)试问在线段AB是否存在一点N,使得MN∥平面BB1C1C,若存在,指出N点位置,并证明你的结论;若不存在,说明理由;
(Ⅱ)求点C1到平面A1ABB1的距离.
考点:点、线、面间的距离计算,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)存在,N点为AB一个靠近A点的三等分点,即AN=
AB,连结BC1,证明MN∥BC1即可;
(Ⅱ)利用VC1-A1AB=VC-A1AB=VA1-CAB,即可求出点C1到平面A1ABB1的距离.
| 1 |
| 3 |
(Ⅱ)利用VC1-A1AB=VC-A1AB=VA1-CAB,即可求出点C1到平面A1ABB1的距离.
解答:
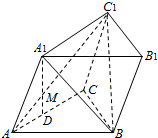 解:(Ⅰ)存在,N点为AB一个靠近A点的三等分点,即AN=
解:(Ⅰ)存在,N点为AB一个靠近A点的三等分点,即AN=
AB.
证明如下:连结BC1,
∵AC∥A1C1,
∴
=
=
=
∴MN∥BC1,
又MN?平面BB1C1C,BC1?平面BB1C1C,
∴MN∥平面BB1C1C.
(Ⅱ)由题意,A1D⊥平面ABC,
∵BC?平面ABC,∴A1D⊥BC.
又BC⊥AC,AC∩AD=D1,
∴BC⊥平面AA1C1C,
又AC1?平面AA1C1C,
∴AC1⊥BC,
又AC1⊥BA1,BA1∩BC=B,
∴AC1⊥平面A1CB
又A1C?平面A1CB,A1C⊥AC1,
∴平行四边形A1C1CA为菱形.
又A1D⊥AC,D为AC的中点,
∴A1A=A1C=AC=BC=a
∵BC⊥平面AA1C1C,
∴∠BCA1=∠BCA=90°,
∴A1B=AB=
a
取AA1中点H,则BH=
a.
∴S△AA1B=
a2,
设点C1到平面A1ABB1的距离为h,
∵C1C∥平面A1ABB1,
∴VC1-A1AB=VC-A1AB=VA1-CAB=
×
a2×
a=
×
a2h,
解得h=
a.
故C1到平面A1ABB1的距离为
a.
 解:(Ⅰ)存在,N点为AB一个靠近A点的三等分点,即AN=
解:(Ⅰ)存在,N点为AB一个靠近A点的三等分点,即AN=| 1 |
| 3 |
证明如下:连结BC1,
∵AC∥A1C1,
∴
| AM |
| MC1 |
| AD |
| A1C1 |
| 1 |
| 2 |
| AN |
| NB |
∴MN∥BC1,
又MN?平面BB1C1C,BC1?平面BB1C1C,
∴MN∥平面BB1C1C.
(Ⅱ)由题意,A1D⊥平面ABC,
∵BC?平面ABC,∴A1D⊥BC.
又BC⊥AC,AC∩AD=D1,
∴BC⊥平面AA1C1C,
又AC1?平面AA1C1C,
∴AC1⊥BC,
又AC1⊥BA1,BA1∩BC=B,
∴AC1⊥平面A1CB
又A1C?平面A1CB,A1C⊥AC1,
∴平行四边形A1C1CA为菱形.
又A1D⊥AC,D为AC的中点,
∴A1A=A1C=AC=BC=a
∵BC⊥平面AA1C1C,
∴∠BCA1=∠BCA=90°,
∴A1B=AB=
| 2 |
取AA1中点H,则BH=
| ||
| 2 |
∴S△AA1B=
| ||
| 4 |
设点C1到平面A1ABB1的距离为h,
∵C1C∥平面A1ABB1,
∴VC1-A1AB=VC-A1AB=VA1-CAB=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| ||
| 4 |
解得h=
| ||
| 7 |
故C1到平面A1ABB1的距离为
| ||
| 7 |
点评:本题考查线面平行,考查线面垂直,考查学生分析解决问题的能力,掌握线面平行、线面垂直、面面垂直的判定定理是关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
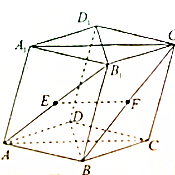 如图所示,四棱柱ABCD-A1B1C1D1中,E、F分别是AB1、BC1的中点,下列结论中,正确的是( )
如图所示,四棱柱ABCD-A1B1C1D1中,E、F分别是AB1、BC1的中点,下列结论中,正确的是( )| A、EF⊥BB1 |
| B、EF∥平面ACC1A1 |
| C、EF⊥BD |
| D、EF⊥平面BCC1B1 |
函数f(x)=2sin
sin(
-
)的最大值等于( )
| x |
| 2 |
| π |
| 3 |
| x |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
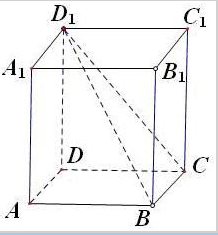 设正方体ABCD-A1B1C1D1的棱长为1,则:
设正方体ABCD-A1B1C1D1的棱长为1,则: