题目内容
11.复数z满足iz=$\frac{2}{1+i}$,则复数z为( )| A. | 1+i | B. | -1-i | C. | -1+i | D. | 1-i |
分析 把已知等式变形,然后利用复数代数形式的乘除运算化简得答案.
解答 解:∵iz=$\frac{2}{1+i}$,
∴z=$\frac{2}{i(1+i)}=\frac{2}{-1+i}=\frac{2(-1-i)}{(-1+i)(-1-i)}=\frac{2(-1-i)}{2}$=-1-i.
故选:B.
点评 本题考查复数代数形式的乘除运算,是基础的计算题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
19.定义在R上的函数f(x),满足f(x+y)=f(x)+f(y)(x,y∈R),且f(1)=2,那么下面四个式子:
①f(1)+2f(1)+…+nf(1);
②$f[\frac{n(n+1)}{2}]$;
③n(n+1);
④n(n+1)f(1)
其中与f(1)+f(2)+…+f(n)(n∈N*)相等的是( )
①f(1)+2f(1)+…+nf(1);
②$f[\frac{n(n+1)}{2}]$;
③n(n+1);
④n(n+1)f(1)
其中与f(1)+f(2)+…+f(n)(n∈N*)相等的是( )
| A. | ①③ | B. | ①② | C. | ①②③④ | D. | ①②③ |
3.设i是虚数单位,则复数z=i(3-4i)的虚部与模的和( )
| A. | 8 | B. | 9 | C. | 5+3i | D. | 5+4i |
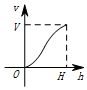
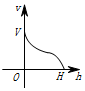
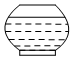 一个高为H,容积为V的鱼缸的轴截面如图所示,向鱼缸里注水,若鱼缸里的水面高度为h时,鱼缸里的水的体积为V',则函数V'=f(h)的大致图象可能是( )
一个高为H,容积为V的鱼缸的轴截面如图所示,向鱼缸里注水,若鱼缸里的水面高度为h时,鱼缸里的水的体积为V',则函数V'=f(h)的大致图象可能是( )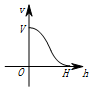
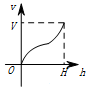
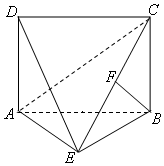 如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.