题目内容
 已知一个几何体的三视图如图所示.
已知一个几何体的三视图如图所示.(Ⅰ)求此几何体的表面积;
(Ⅱ)在如图的正视图中,如果点A为所在线段中点,点B为顶点,求在几何体侧面上从点A到点B的最短路径的长.
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:(I)几何体是一个圆锥与一个圆柱的组合体,由三视图判断圆锥与圆柱的底面半径与母线长,根据其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和,代入公式计算;
(II)利用圆柱的侧面展开图,求得EB的长,再利用勾股定理求AB的圆柱面距离.
(II)利用圆柱的侧面展开图,求得EB的长,再利用勾股定理求AB的圆柱面距离.
解答:
解:(Ⅰ)由三视图知:几何体是一个圆锥与一个圆柱的组合体,且圆锥与圆柱的底面半径为2,母线长分别为2
、4,
其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.
S圆锥侧=
×2π×2×2
=4
π;
S圆柱侧=2π×2×4=16π;
S圆柱底=π×22=4π.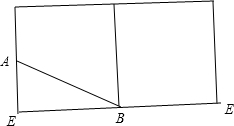
∴几何体的表面积S=20π+4
π;
(Ⅱ)沿A点与B点所在母线剪开圆柱侧面,如图:
则AB=
=
=2
,
∴以从A点到B点在侧面上的最短路径的长为2
.
| 2 |
其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.
S圆锥侧=
| 1 |
| 2 |
| 2 |
| 2 |
S圆柱侧=2π×2×4=16π;
S圆柱底=π×22=4π.

∴几何体的表面积S=20π+4
| 2 |
(Ⅱ)沿A点与B点所在母线剪开圆柱侧面,如图:
则AB=
| EA2+EB2 |
| 22+(2π)2 |
| 1+π2 |
∴以从A点到B点在侧面上的最短路径的长为2
| 1+π2 |
点评:本题考查了由三视图求几何体的表面积与体积,考查了圆柱面上两点的最短距离问题,根据三视图判断几何体的形状及数据所对应的几何量是解答此类问题的关键.

练习册系列答案
相关题目
若n=
2xdx,则(x-
)n的展开式中常数项为( )
| ∫ | 2 0 |
| 1 |
| 2x |
A、
| ||
B、-
| ||
C、
| ||
D、-
|