题目内容
正项数列{an}满足:an2-(2n-1)an-2n=0.
(1)求数列{an}的通项公式an;
(2)令bn=
,求数列{bn}的前n项和Tn.并求使Tn>
成立的最小正整数n的值.
(1)求数列{an}的通项公式an;
(2)令bn=
| 1 |
| (n+1)an |
| 5 |
| 11 |
考点:数列的求和,数列递推式
专题:点列、递归数列与数学归纳法
分析:(1)根据数列的递推关系,即可求数列{an}的通项公式an;
(2)求出bn=
的通项公式,利用裂项法即可得到结论.
(2)求出bn=
| 1 |
| (n+1)an |
解答:
解:(1)∵an2-(2n-1)an-2n=0,
∴(an-2n)(an+1)=0,
又∵各项为正,∴an=2n.
(2)∵bn=
=
=
(
-
),
∴数列{bn}的前n项和Tn=
(1-
+
-
+…+
-
)=
(1-
),
若Tn>
,即
(1-
)>
,
解得n>10,即使Tn>
成立的最小正整数n=11.
∴(an-2n)(an+1)=0,
又∵各项为正,∴an=2n.
(2)∵bn=
| 1 |
| (n+1)an |
| 1 |
| 2n(n+1) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
∴数列{bn}的前n项和Tn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| n+1 |
若Tn>
| 5 |
| 11 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 5 |
| 11 |
解得n>10,即使Tn>
| 5 |
| 11 |
点评:本题主要考查数列的通项公式以及数列求和,利用裂项法是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
复数
的值是( )
| 2-i |
| 3-4i |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
椭圆a2x2-
y2=1的一个焦点是(-2,0),则a等于( )
| a |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列命题是真命题的是( )
| A、a>b是ac2>bc2的充要条件 |
| B、a>1,b>1是ab>1的充分条件 |
| C、?x0∈R,e x0≤0 |
| D、若p∨q为真命题,则p∧q为真 |
已知x,y∈R,若lne-1i+2=y+xi,则x3+y=( )
| A、9 | B、3 | C、1 | D、2 |
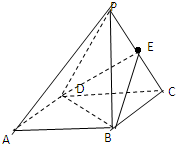 如图,在四棱锥P-ABCD中,底面ABCD为正方形,E是PC的中点,
如图,在四棱锥P-ABCD中,底面ABCD为正方形,E是PC的中点,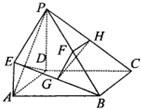 如图所示,ABCD是边长为2的正方形,PD⊥平面ABCD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.
如图所示,ABCD是边长为2的正方形,PD⊥平面ABCD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.