题目内容

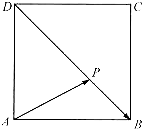如图，点P为正方形ABCD对角线BD上的点，若
AP
•
PB
的最大值为2，则该正方形的边长为（　　）
A、4
2
B、4
C、2
2
D、2
考点：平面向量数量积的运算
专题：平面向量及应用
分析：设该正方形的边长为a，建立如图所示的直角坐标系．利用向量的坐标运算、数量积运算和二次函数的单调性即可得出．
解答： 解：设该正方形的边长为a，建立如图所示的直角坐标系．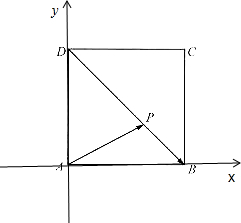
设
BP
=λ
BD
，
则
AP
=
AB
+λ(
AD
-
AB
)
=(1-λ)
AB
+λ
AD

=（1-λ）（a，0）+λ（0，a）
=（a-λa，λa）．
∴
PB
=
AB
-
AP
=（a，0）-（a-λa，λa）=（λa，-λa）．
∴
AP
•
PB
=λa（a-λa）-λ2a2=-2λ2a2+λa2=-2a2(λ-
1
4
)2+
1
8
a2≤
1
8
a2，当且仅当λ=
1
4
时取等号．
∵
AP
•
PB
的最大值为2，∴
1
8
a2=2，解得a=4．
故选：B．
点评：本题考查了向量的坐标运算、数量积运算和二次函数的单调性，属于中档题．
练习册系列答案
相关题目
若（ax2+
1
x
）5的展开式中x4的系数为80，则实数a=
 
．
△ABC中，设角A，B，C的对边分别为a，b，c，若c=2，b=1，B=30°，则C=
 
．
设抛物线y2=4x的交点为F，顶点为O，M是抛物线上的动点，则
|MO|
|MF|
的最大值为（　　）
A、
3
3
B、
2
3
3
C、
4
3
D、
3
设随机变量X服从正态分布N（3，4），若P（X＜2a+3）=P（X＞a-2），则a的值为（　　）
A、
5
3
B、3
C、5
D、
7
3
在集合M={1，2，3，4}的所有非空子集中，任取一个集合，恰好满足条件“?x∈A，则6-x∈A”的集合的概率是（　　）
A、
4
15
B、
1
5
C、
2
15
D、
2
3
设等差数列{an}的前n项和Sn，若S13=26，S14=-14，则Sn取最大值时，n的值为（　　）
A、7B、8C、9D、14
已知圆C的内接正三角形的边长为
3
，且圆心为直线x-y+1=0与x轴的交点，则圆C的方程为（　　）
A、（x-1）2+y2=1
B、（x-1）2+y2=4
C、（x+1）2+y2=1
D、（x+1）2+y2=4
设x2+x7=a0+a1（x+1）+a2（x+1）2+…+a6（x+1）6+a7（x+1）7，则a6=（　　）
A、-5B、-6C、-7D、-8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网