题目内容
设x2+x7=a0+a1(x+1)+a2(x+1)2+…+a6(x+1)6+a7(x+1)7,则a6=( )
| A、-5 | B、-6 | C、-7 | D、-8 |
考点:二项式系数的性质
专题:二项式定理
分析:根据 x2+x7=[-1+(x+1)]2+[-1+(x+1)]7=a0+a1(x+1)+a2(x+1)2+…+a6(x+1)6+a7(x+1)7,可得a6=
•(-1),计算求得结果.
| C | 6 7 |
解答:
解:∵x2+x7=[-1+(x+1)]2+[-1+(x+1)]7=a0+a1(x+1)+a2(x+1)2+…+a6(x+1)6+a7(x+1)7,
则 a6=
•(-1)=-7,
故选:C.
则 a6=
| C | 6 7 |
故选:C.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
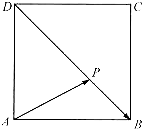 如图,点P为正方形ABCD对角线BD上的点,若
如图,点P为正方形ABCD对角线BD上的点,若| AP |
| PB |
A、4
| ||
| B、4 | ||
C、2
| ||
| D、2 |
已知抛物线的焦点坐标是(0,
),则它的标准方程是( )
| 1 |
| 2 |
| A、y2=x |
| B、x2=2y |
| C、x2=y |
| D、y2=2x |
直线y=-x+1的倾斜角为( )
| A、30° | B、45° |
| C、135° | D、150° |
一个总体分为A,B,C三层,其个体数之比为5:2:3,若用分层抽样的方式抽取容量为200的样本,则应从B中抽取的个体数为( )
| A、20 | B、40 | C、60 | D、80 |
定义
?
=
,若
=(1,2),
=(3,-2),则与
?
反向的向量为( )
| a |
| b |
| ||||
|
| a |
| b |
| a |
| b |
| A、(5,-6) |
| B、(5,6) |
| C、(-5,6) |
| D、(-5,-6) |