题目内容
设抛物线y2=4x的交点为F,顶点为O,M是抛物线上的动点,则
的最大值为( )
| |MO| |
| |MF| |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设M到准线的距离等于d,由抛物线的定义可得
=
=
=
,令2m-1=t,利用基本不等式求得最大值.
| |MO| |
| |MF| |
| |MO| |
| d |
| ||
| m+1 |
1+
|
解答:
解:焦点F(1,0),设M(m,n),则n2=4m,m>0,设M 到准线x=-1的距离等于d,
则
=
=
=
.
令2m-1=t,t>-1,则m=
(t+1),
∴
=
≤
=
(当且仅当t=3时,等号成立).
故
的最大值为
,
故选:B.
则
| |MO| |
| |MF| |
| |MO| |
| d |
| ||
| m+1 |
1+
|
令2m-1=t,t>-1,则m=
| 1 |
| 2 |
∴
| |MO| |
| |MF| |
1+
|
1+
|
2
| ||
| 3 |
故
| |MO| |
| |MF| |
2
| ||
| 3 |
故选:B.
点评:本题考查抛物线的定义、简单性质,基本不等式的应用,体现了换元的思想,把
化为
,是解题的关键和难点,属于中档题.
| |MO| |
| |MF| |
1+
|

练习册系列答案
相关题目
下面结论正确的是( )
A、若a<b,则有
| ||||
B、若a>b,则有
| ||||
| C、若a>b,则有a+c>b+c | ||||
| D、若a>b,则|a|>b |
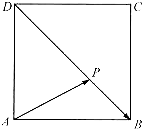 如图,点P为正方形ABCD对角线BD上的点,若
如图,点P为正方形ABCD对角线BD上的点,若| AP |
| PB |
A、4
| ||
| B、4 | ||
C、2
| ||
| D、2 |
等差数列{an}中,a1=1,a3=4,则公差d等于( )
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
直线y=-x+1的倾斜角为( )
| A、30° | B、45° |
| C、135° | D、150° |