题目内容
设等差数列{an}的前n项和Sn，若S13=26，S14=-14，则Sn取最大值时，n的值为（ ）
| A、7 | B、8 | C、9 | D、14 |
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：利用等差数列的前n项和公式求出首项和公差，由此求出等差数列的前n项和公式，利用配方法能求出Sn取最大值时，n的值．
解答：
解：∵等差数列{an}的前n项和Sn，S13=26，S14=-14，
∴
，
解得a1=38，d=-6，
∴Sn=38n+
×(-6)
=-3n2+41n
=-3（n-
）2+
．
∵n∈N*，∴n=7时，Sn取最大值．
故选：A．
∴
|
解得a1=38，d=-6，
∴Sn=38n+
| n(n-1) |
| 2 |
=-3n2+41n
=-3（n-
| 41 |
| 6 |
| 1681 |
| 12 |
∵n∈N*，∴n=7时，Sn取最大值．
故选：A．
点评：本题考查Sn取最大值时，n的值的求法，是基础题，解题时要认真审题，注意配方法的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
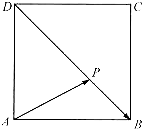如图，点P为正方形ABCD对角线BD上的点，若| AP |
| PB |
A、4
| ||
| B、4 | ||
C、2
| ||
| D、2 |
已知f（x）是定义在R上的单调递减的函数，则不等式f（a2-4）＞f（3a）的解集为（ ）
| A、（2，6） |
| B、（-1，4） |
| C、（1，4） |
| D、（-3，5） |
等差数列{an}中，a1=1，a3=4，则公差d等于（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
已知tanx=5，则
=（ ）
| sinx+3cosx |
| sinx-cosx |
| A、1 | B、2 | C、3 | D、4 |
已知抛物线的焦点坐标是（0，
），则它的标准方程是（ ）
| 1 |
| 2 |
| A、y2=x |
| B、x2=2y |
| C、x2=y |
| D、y2=2x |