题目内容
10．曲线x2-2xy+y2+4x-8y+12=0的范围是x≥-1，y≥2．分析 由题意，令x=t2-2t，则y=t2+2，即可得出结论．
解答 解：由题意，令x=t2-2t，则y=t2+2，
x=t2-2t=（t-1）2-1≥-1，y=t2+2≥2
∴曲线x2-2xy+y2+4x-8y+12=0的范围是x≥-1，y≥2．
故答案为：x≥-1，y≥2．
点评 本题考查曲线与方程，考查学生的计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
9．已知全集U={0，1，2，3，4}，M={2，3，4}，N={0，1，2，3}，则图中阴影部分所表示的集合为（ ）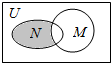
| A． | {2，3} | B． | {0，1，2} | C． | {1，2，3} | D． | {0，1} |