题目内容

18．已知等差数列{an}中，a1+a2+a3+…a100=0，则（　　）
A．a1+a101＞0B．a2+a100＜0C．a3+a98=0D．a5=51

分析 直接利用等差数列的性质求解即可．

解答 解：等差数列{an}中，a1+a2+a3+…+a100=50（a1+a100）=50（a3+a98）=0．
故选：C．

点评 本题考查等差数列的简单性质的应用，是基础题．

练习册系列答案
相关题目
6．已知数列满足an+1=2an+3×2n，a1=2，求数列的通项公式．
9．已知集合A={x||x-a|≤4}，集合B={x|x2-4x-5＞0}
（1）若A∩B=（5，7]，求实数a的值；  
（2）若A∩B=A，求实数a的取值范围．
6．已知f（x）=2sin（2x+$\frac{π}{3}$），
（Ⅰ）求f（x）图象的对称轴方程；
（Ⅱ）若将函数f（x）的图象向右平移$\frac{π}{4}$个单位长度后得到函数g（x）的图象，请写出函数g（x）的解析式；
（Ⅲ）请通过列表、描点、连线，在所给的平面直角坐标系中画出函数g（x）在[0，π]上的简图．
13．在棱长为2的正方体中随机取一点，该点落在这个正方体的内切球内的概率是$\frac{π}{6}$．
3．如图，正方形ABCD中，E为DC的中点，若$\overrightarrow{AD}=λ\overrightarrow{AC}+μ\overrightarrow{AE}$，则λ-μ的值为（　　）
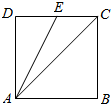
A．3B．2C．1D．-3
10．过椭圆$\frac{x^2}{9}+\frac{y^2}{16}=1$的一个焦点F1的弦AB与另一个焦点F2围成的三角形△ABF2的周长是16．
7．已知函数f（x）=2sinxcosx+cos2x-sin2x．
（I）求f（x）的最小正周期；
（Ⅱ）求f（x）的单调递增区间．
8．设$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$是平面捏一组基底，则下面四组向量中，能作为基底的是（　　）
A．$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$与$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$B．2$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$与-4$\overrightarrow{{e}_{′1}}$-6$\overrightarrow{{e}_{2}}$
C．$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$与$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$D．-$\frac{1}{2}$$\overrightarrow{{e}_{1}}$+$\frac{1}{8}$$\overrightarrow{{e}_{2}}$与$\overrightarrow{{e}_{1}}$-$\frac{1}{4}$$\overrightarrow{{e}_{2}}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网