题目内容
已知共焦点F1,F2的椭圆与双曲线,它们的一个公共点是P,若
•
=0,椭圆的离心率e1与双曲线的离心率e2的关系式为( )
| F1P |
| F2P |
A、
| ||||
B、
| ||||
| C、e12+e22=2 | ||||
| D、e22-e12=2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设椭圆与双曲线的方程分别为:
+
=1,
-
=1.设|PF1|=m,|PF2|=n.利用椭圆和双曲线的定义可得:m+n=2a1,m-n=2a2.两边平方可得4
+4
=(m+n)2+(m-n)2=2(m2+n2),由
•
=0,可得F1P⊥F2P.再利用勾股定理可得m2+n2=(2c)2=4c2,再利用离心率计算公式即可得出.
| x2 | ||
|
| y2 | ||
|
| x2 | ||
|
| y2 | ||
|
| a | 2 1 |
| a | 2 2 |
| F1P |
| F2P |
解答:
解:如图所示,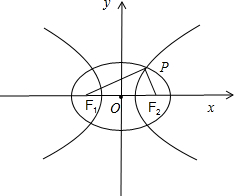
设椭圆与双曲线的方程分别为:
+
=1,
-
=1.
其中a1>b1>0,a2>0,b2>0,
-
=c2=
+
.
设|PF1|=m,|PF2|=n.
则m+n=2a1,m-n=2a2.
∴4
+4
=(m+n)2+(m-n)2=2(m2+n2),
∵
•
=0,∴F1P⊥F2P.
∴m2+n2=(2c)2=4c2,
∴4
+4
=2×4c2,
∴
+
=2c2.
∴
+
=
+
=2.
故选:A.

设椭圆与双曲线的方程分别为:
| x2 | ||
|
| y2 | ||
|
| x2 | ||
|
| y2 | ||
|
其中a1>b1>0,a2>0,b2>0,
| a | 2 1 |
| b | 2 1 |
| a | 2 2 |
| b | 2 2 |
设|PF1|=m,|PF2|=n.
则m+n=2a1,m-n=2a2.
∴4
| a | 2 1 |
| a | 2 2 |
∵
| F1P |
| F2P |
∴m2+n2=(2c)2=4c2,
∴4
| a | 2 1 |
| a | 2 2 |
∴
| a | 2 1 |
| a | 2 2 |
∴
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||
|
| 1 | ||
|
故选:A.
点评:本题考查了椭圆与双曲线的定义、标准方程及其性质、向量垂直与数量积的关系等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到如下的2×2列联表.
则至少有( )的把握认为喜爱打篮球与性别有关.
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| A、95% | B、99% |
| C、99.5% | D、99.9% |
i是虚数单位,复数
的虚部为( )
| -2i |
| 1+i |
| A、2 | B、-1 | C、1 | D、-2 |
已知集合U={-1,0,1},A={1},B⊆U,则B∩(∁UA)不可能为( )
| A、∅ | B、{0} |
| C、{-1,0} | D、{-1,0,1} |
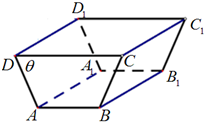 某农户准备建一个水平放置的直四棱柱形储水窖(如图),其中直四棱柱的高AA1=10m,两底面ABCD,A1B1C1D1是高为2m,面积为10m2的等腰梯形,且∠ADC=θ(0<θ<
某农户准备建一个水平放置的直四棱柱形储水窖(如图),其中直四棱柱的高AA1=10m,两底面ABCD,A1B1C1D1是高为2m,面积为10m2的等腰梯形,且∠ADC=θ(0<θ<