Question

定义，max{m，n}=

m，m≥n n，m＜n

，已知函数f（x）=max{x²-2x，2a-2x}，a∈R
（1）当a=1时，直接写出函数f（x）的单调区间，并求出函数f（x）的最小值
（2）求函数f（x）的值域．

Answer 1

考点：函数的最值及其几何意义,函数单调性的判断与证明

专题：计算题,作图题,函数的性质及应用

分析：（1）当a=1时，化简f（x）=max{x²-2x，2-2x}=

x2-2x，x≤- 2 2-2x，- 2 ＜x＜ 2 x2-2x，x≥ 2

，从而写出单调区间及最小值；
（2）令x²-2x=2a-2x得x²=2a；故当a=0时，方程仅有一个解；从而讨论确定函数的值域．

解答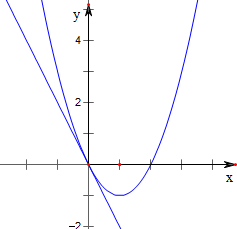： 解：（1）当a=1时，
f（x）=max{x²-2x，2-2x}=

x2-2x，x≤- 2 2-2x，- 2 ＜x＜ 2 x2-2x，x≥ 2

，
故函数f（x）的单调减区间为（-∞，

2

），
单调增区间为（

2

，+∞）；
其最小值为f（

2

）=2-2

2

；
（2）令x²-2x=2a-2x得x²=2a；
故当a=0时，方程仅有一个解；
故当a≤0时，f（x）=max{x²-2x，2-2x}
=x²-2x=（x-1）²-1；
故函数f（x）的值域为[-1，+∞）；
当a＞0时，令x²=2a解得，
x=-

2a

或x=

2a

；
故函数f（x）的单调减区间为（-∞，

2a

），
单调增区间为（

2a

，+∞）；
故f（x）≥f（

2a

）=2a-2

2a

；
故f（x）的值域为[2a-2

2a

，+∞）．

点评：本题考查了分段函数的应用及分类讨论的应用，同时考查了数形结合的应用，属于中档题．