题目内容
如图,在直三棱柱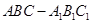 中,D、E分别是BC和
中,D、E分别是BC和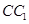 的中点,已知AB=AC=AA1=4,ÐBAC=90°.
的中点,已知AB=AC=AA1=4,ÐBAC=90°.
(1)求证: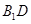 ⊥平面
⊥平面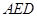 ;
;
(2)求二面角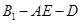 的余弦值;
的余弦值;
(3)求三棱锥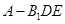 的体积.
的体积.
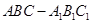 中,D、E分别是BC和
中,D、E分别是BC和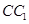 的中点,已知AB=AC=AA1=4,ÐBAC=90°.
的中点,已知AB=AC=AA1=4,ÐBAC=90°.
(1)求证:
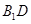 ⊥平面
⊥平面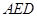 ;
;(2)求二面角
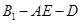 的余弦值;
的余弦值;(3)求三棱锥
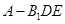 的体积.
的体积.(1)见解析 (2) (3)8
(3)8
 (3)8
(3)8试题分析:
(1)(2)(3)均可利用坐标法,即分别以
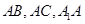 建立三维空间坐标系.下面重点分析法2
建立三维空间坐标系.下面重点分析法2(1)利用勾股定理可以求的线段
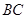 的长,而要证明
的长,而要证明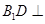 面
面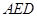 ,只需要证明
,只需要证明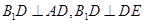 ,首先可以三次利用勾股定理把
,首先可以三次利用勾股定理把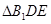 的三条边长求出,再利用勾股定理证明
的三条边长求出,再利用勾股定理证明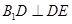 ,线段
,线段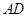 为等腰直角三角形ABC的三线合一即有
为等腰直角三角形ABC的三线合一即有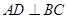 ,可得到
,可得到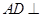 面
面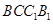 ,进而得到
,进而得到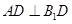 ,即可通过线线垂直证明
,即可通过线线垂直证明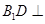 面DAE.
面DAE.(2)要求二面角
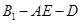 的余弦值,需要作出该二面角的平面角,为此过D做DM⊥AE于点M,连接B1M.,根据第一问有
的余弦值,需要作出该二面角的平面角,为此过D做DM⊥AE于点M,连接B1M.,根据第一问有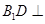 面AED且
面AED且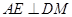 可以得到
可以得到 面
面 ,则
,则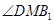 即为所求二面角的平面角,即该角的余弦值为
即为所求二面角的平面角,即该角的余弦值为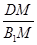 .利用勾股定理即可得到
.利用勾股定理即可得到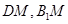 的长,进而得到二面角的余弦值.
的长,进而得到二面角的余弦值.(3)由(1)可得
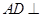 面
面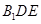 ,则该三棱锥可以以
,则该三棱锥可以以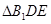 作为底面,高为
作为底面,高为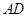 来求的体积,而AD和三角形的面积都可以用勾股定理求的.
来求的体积,而AD和三角形的面积都可以用勾股定理求的.试题解析:
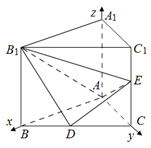
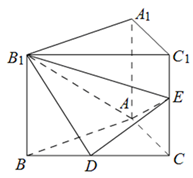
法1:依题意,建立如图所示的空间直角坐标系A-xyz.因为
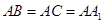 =4,所以A(0,0,0),B(4,0,0),E(0,4,2),D(2,2,0),B1(4,0,4). (1分)
=4,所以A(0,0,0),B(4,0,0),E(0,4,2),D(2,2,0),B1(4,0,4). (1分)(1)
 ,
,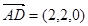 ,
,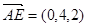 . (2分)
. (2分)因为
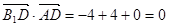 ,所以
,所以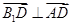 ,即
,即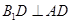 . (3分)
. (3分)因为
 ,所以
,所以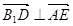 ,即
,即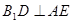 . (4分)
. (4分)又AD、AEÌ平面AED,且AD∩AE=A,故
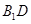 ⊥平面
⊥平面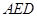 . (5分)
. (5分)(2)由(1)知
 为平面AED的一个法向量. (6分)
为平面AED的一个法向量. (6分)设平面 B1AE的法向量为
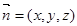 ,因为
,因为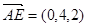 ,
,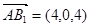 ,
,所以由
 ,得
,得 ,令y=1,得x=2,z=-2.即
,令y=1,得x=2,z=-2.即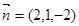 .(7分)
.(7分)∴
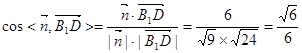 , (8分)
, (8分)∴二面角
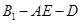 的余弦值为
的余弦值为 . (9分)
. (9分)(3)由
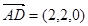 ,
,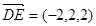 ,得
,得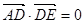 ,所以AD⊥DE. (10分)
,所以AD⊥DE. (10分)由
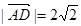 ,
,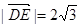 ,得
,得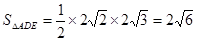 . (11分)
. (11分)由(1)得B1D为三棱锥B1-ADE的高,且
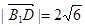 , (12分)
, (12分)所以
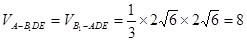 . (13分)
. (13分)法2:依题意得,
 平面ABC,
平面ABC,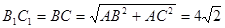 ,
,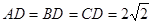 ,
,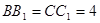 ,
,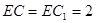 .
.(1)∵
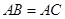 ,D为BC的中点,∴AD⊥BC.
,D为BC的中点,∴AD⊥BC. ∵B1B⊥平面ABC,AD
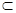 平面ABC,∴AD⊥B1B.
平面ABC,∴AD⊥B1B. BC、B1B
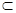 平面B1BCC1,且BC∩B1B=B,所以AD⊥平面B1BCC1.
平面B1BCC1,且BC∩B1B=B,所以AD⊥平面B1BCC1.又B1D
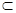 平面B1BCC1,故B1D⊥AD . (2分)
平面B1BCC1,故B1D⊥AD . (2分)由
 ,
,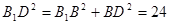 ,
,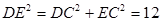 ,
,得
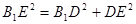 ,所以
,所以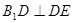 . (4分)
. (4分)又AD、DE
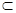 平面AED,且AD∩DE=E,故
平面AED,且AD∩DE=E,故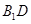 ⊥平面
⊥平面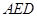 . (5分)
. (5分)(2)过D做DM⊥AE于点M,连接B1M.
由B1D⊥平面AED,AE
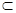 平面AED,得AE ⊥B1D.
平面AED,得AE ⊥B1D.又B1D、DM
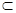 平面B1DM,且B1D∩DM=D,故AE⊥平面B1DM.
平面B1DM,且B1D∩DM=D,故AE⊥平面B1DM.因为B1M
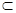 平面B1DM,所以B1M⊥AE.
平面B1DM,所以B1M⊥AE.故∠B1MD为二面角B1—AE—D的平面角. (7分)
由(1)得,AD⊥平面B1BCC1,又DE
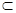 平面B1BCC1,所以AD⊥DE.
平面B1BCC1,所以AD⊥DE.在Rt△AED中,
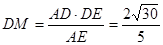 , (8分)
, (8分)在Rt△B1DM中,
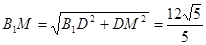 ,
,所以
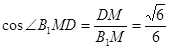 ,即二面角B1—AE—D的余弦值为
,即二面角B1—AE—D的余弦值为 . (9分)
. (9分)(3)由(1)得,AD⊥平面B1BCC1,
所以AD为三棱锥A-B1DE的高,且
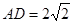 . (10分)
. (10分)由(1)得
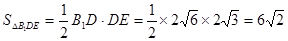 . (11分)
. (11分)故
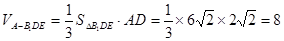 . (13分)
. (13分)
练习册系列答案
相关题目

 中,
中, 底面
底面 ,
, ,E、F分别是棱
,E、F分别是棱 的中点.
的中点. 上的点
上的点 满足平面
满足平面 //平面
//平面 ,试确定点
,试确定点 ⊥A1C.
⊥A1C.
 的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
 平面
平面 ;
; 的大小;
的大小; 与平面
与平面
 平面
平面 .
. 平面
平面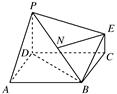

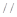 平面
平面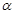 ,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面
,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面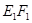 长的范围是( )
长的范围是( ) ]
] ,
, ,
, ,
,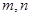 是两条不同的直线,
是两条不同的直线,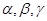 是三个不同的平面,则下列命题中正确命题是( )
是三个不同的平面,则下列命题中正确命题是( )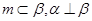 ,则
,则
 ,
,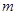 ∥
∥ ,则
,则 ∥
∥
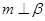 ,
,
 则
则
 中,
中, 分别是
分别是 的中点,则四边形
的中点,则四边形 是( )
是( )