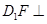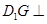题目内容
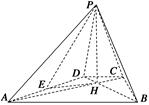
如图,三棱柱 的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。

(1)求证: 平面
平面 ;
;
(2)求二面角 的大小;
的大小;
(3)求直线 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
 的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
(1)求证:
 平面
平面 ;
;(2)求二面角
 的大小;
的大小;(3)求直线
 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.(1)见解析(2)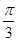 (3)
(3)
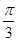 (3)
(3)
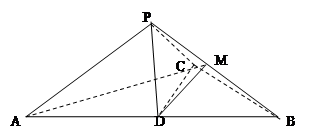
试题分析:(1)由题意及题中P为AB1中点和D为AC中点,中点这样信息,得到线线PD∥B1C平行,在利用PD∥平面A1BD线面平行,利用线面平行的判定定理得到线面B1C∥平面A1BD平行;
(2)有正三棱柱及二面角平面角的定义,找到二面角的平面角,然后再三角形中解出二面角的大小;
(3)利用条件及上两问的证题过成找到∠APM就是直线A1B与平面A1BD所成的线面角,然后再三角形中解出即可.
试题解析:解法一:
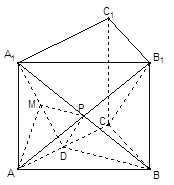
(1)设
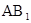 与
与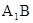 相交于点P,连接PD,则P为
相交于点P,连接PD,则P为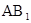 中点 1分
中点 1分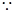 D为AC中点,
D为AC中点,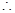 PD//
PD//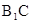 , 3分
, 3分又
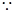 PD
PD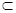 平面
平面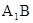 D,
D,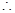
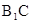 //平面
//平面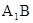 D 4分
D 4分(2)
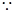 正三棱住
正三棱住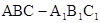 ,
,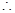
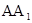
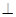 底面ABC,又
底面ABC,又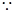 BD
BD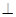 AC,
AC,
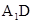
 BD,
BD,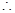
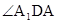 就是二面角
就是二面角 的平面角 6分
的平面角 6分
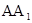 =
=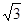 ,AD=
,AD=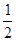 AC=1,
AC=1,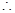 tan
tan 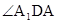 =
=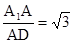
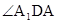 =
=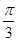 , 即二面角
, 即二面角 的大小是
的大小是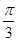 8分
8分(3)由(2)作AM
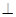
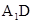 ,M为垂足 9分
,M为垂足 9分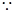 BD
BD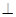 AC,平面
AC,平面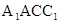
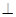 平面ABC,平面
平面ABC,平面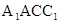
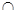 平面ABC=AC
平面ABC=AC BD
BD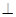 平面
平面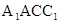 ,
, AM
AM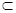 平面
平面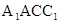 ,
,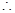 BD
BD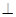 AM
AM又
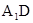
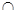 BD = D,
BD = D,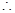 AM
AM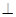 平面
平面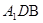 , 10分
, 10分连接MP,则
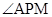 就是直线
就是直线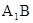 与平面
与平面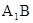 D所成的角 11分
D所成的角 11分
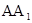 =
=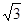 ,AD=1,
,AD=1, 在Rt
在Rt
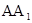 D中,
D中,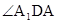 =
=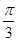 ,
,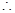
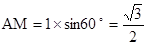 ,
,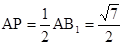 ,
,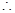
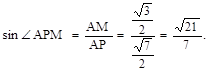
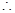 直线
直线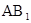 与平面
与平面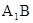 D所成的角的正弦值为
D所成的角的正弦值为 13分
13分解法二:
(1)同解法一 4分
(2)如图建立空间直角坐标系,
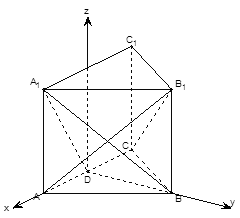
则D(0,0,0),A(1,0,0),
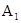 (1,0,
(1,0,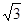 ),B(0,
),B(0,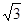 ,0),
,0),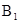 (0,
(0,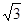 ,
,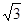 )
)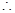
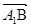 =(
=(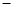 1,
1,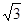 ,
,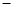
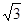 ),
),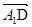 =(
=(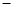 1,0,
1,0,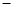
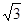 ) 5分
) 5分设平面
 的法向量为n=(x,y,z)
的法向量为n=(x,y,z)则n
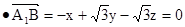
n
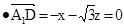 ,则有
,则有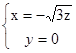 ,得n=(
,得n=(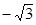 ,0,1) 6分
,0,1) 6分由题意,知
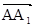 =(0,0,
=(0,0,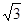 )是平面ABD的一个法向量.
)是平面ABD的一个法向量.设n与
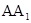 所成角为
所成角为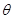 ,则
,则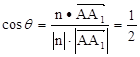 , 7分
, 7分又
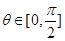 ,
,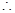
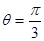 ,即二面角
,即二面角 的大小是
的大小是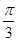 8分
8分(3)由已知得
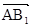 =(
=(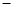 1,
1,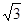 ,
,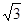 ), n=(
), n=(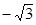 ,0,1) 9分
,0,1) 9分则
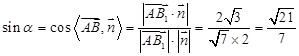 12分
12分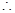 直线
直线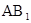 与平面
与平面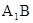 D所成的角的正弦值为
D所成的角的正弦值为 13分
13分
练习册系列答案
相关题目
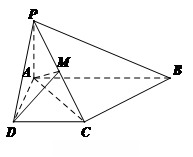
 .
.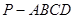 中,
中,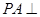 平面
平面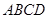 ,底面
,底面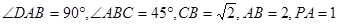 .
.
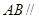 平面
平面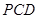 ;
;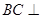 平面
平面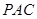 ;
;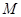 是
是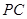 的中点,求三棱锥
的中点,求三棱锥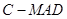 的体积.
的体积. 中,D、E分别是BC和
中,D、E分别是BC和 的中点,已知AB=AC=AA1=4,ÐBAC=90°.
的中点,已知AB=AC=AA1=4,ÐBAC=90°.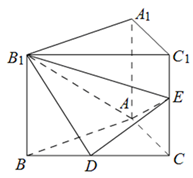
 ⊥平面
⊥平面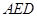 ;
;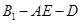 的余弦值;
的余弦值;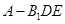 的体积.
的体积.
 平面PBC ②平面
平面PBC ②平面 //平面
//平面 ,直线
,直线 平面
平面
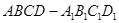 ,点
,点 ,
,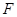 ,
,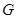 分别是线段
分别是线段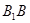 ,
,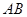 和
和 上的动点,观察直线
上的动点,观察直线 与
与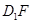 ,
,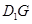 .给出下列结论:
.给出下列结论: