题目内容
正四面体ABCD的棱长为1,其中线段AB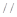 平面
平面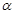 ,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面
,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面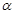 上的射影
上的射影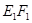 长的范围是( )
长的范围是( )
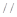 平面
平面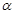 ,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面
,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面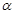 上的射影
上的射影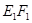 长的范围是( )
长的范围是( )A.[0, ] ] | B.[ , , ] ] |
C.[ , , ] ] | D.[ , , ] ] |
D
试题分析:

如图,取AC中点为G,结合已知可得GF
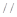 AB,在正四面体中,AB
AB,在正四面体中,AB CD,又GE
CD,又GE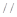 CD,所以GE
CD,所以GE GF,所以
GF,所以 ,当四面体绕AB旋转时,因为GF
,当四面体绕AB旋转时,因为GF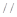 平面
平面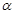 ,GE与GF的垂直性保持不变,显然,当CD与平面
,GE与GF的垂直性保持不变,显然,当CD与平面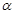 垂直时,GE在平面上的射影长最短为0,此时EF在平面
垂直时,GE在平面上的射影长最短为0,此时EF在平面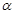 上的射影
上的射影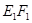 的长取得最小值
的长取得最小值 ,当CD与平面
,当CD与平面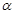 平行时,GE在平面上的射影长最长为
平行时,GE在平面上的射影长最长为 ,
,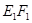 取得最大值
取得最大值 ,所以射影
,所以射影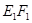 长的取值范围是 [
长的取值范围是 [ ,
, ],故选D
],故选D
练习册系列答案
相关题目
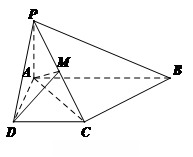
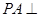 平面ABCD,AD//BC,
平面ABCD,AD//BC,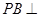 AC,
AC,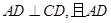
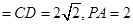 ,点M在线段PD上.
,点M在线段PD上.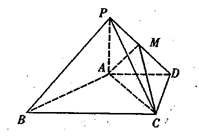
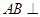 平面PAC;
平面PAC;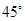 ,试确定点M的位置.
,试确定点M的位置.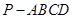 中,
中,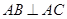 ,
,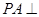 平面
平面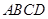 ,且
,且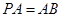 ,点
,点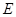 是
是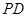 的中点.
的中点.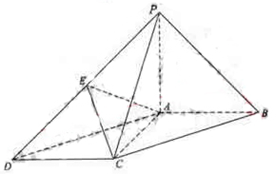
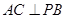 ;
;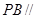 平面
平面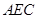 ;
;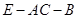 的大小.
的大小.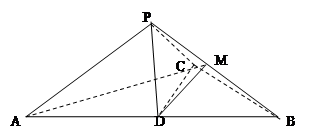 .
.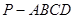 中,
中,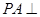 平面
平面 ,底面
,底面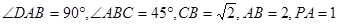 .
.
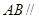 平面
平面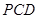 ;
;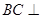 平面
平面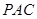 ;
;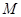 是
是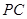 的中点,求三棱锥
的中点,求三棱锥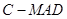 的体积.
的体积.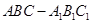 中,D、E分别是BC和
中,D、E分别是BC和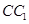 的中点,已知AB=AC=AA1=4,ÐBAC=90°.
的中点,已知AB=AC=AA1=4,ÐBAC=90°.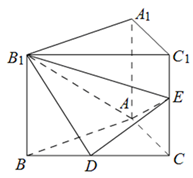
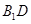 ⊥平面
⊥平面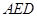 ;
;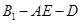 的余弦值;
的余弦值;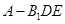 的体积.
的体积.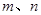 是不同的直线,
是不同的直线,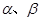 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题: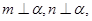 则
则
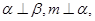 则
则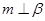
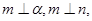 则
则
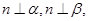 则
则

 平面PBC ②平面
平面PBC ②平面 .
.