题目内容
20.过点M(2,-1)作斜率为$\frac{1}{2}$的直线与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A,B两个不同点,若M是AB的中点,则该椭圆的离心率e=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{4}$ |
分析 利用点差法,结合M是线段AB的中点,斜率为$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{2{b}^{2}}{{a}^{2}}$=$\frac{1}{2}$,即可求出椭圆的离心率.
解答 解:设A(x1,y1),B(x2,y2),则x1+x2=4,y1+y2=-2,
A,B两个不同点代入椭圆方程,可得$\frac{{{x}_{1}}^{2}}{{a}^{2}}$+$\frac{{{y}_{1}}^{2}}{{b}^{2}}$=1,$\frac{{{x}_{2}}^{2}}{{a}^{2}}$+$\frac{{{y}_{2}}^{2}}{{b}^{2}}$=1,
作差整理可得$\frac{4({x}_{1}-{x}_{2})}{{a}^{2}}$+$\frac{-2({y}_{1}-{y}_{2})}{{b}^{2}}$=0,
∵斜率为$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{2{b}^{2}}{{a}^{2}}$=$\frac{1}{2}$,
∴a=2b,
∴c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{3}$b,
∴e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$.
故选:C.
点评 本题考查椭圆的离心率,考查学生的计算能力,正确运用点差法是关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.经过点A(5,2),B(3,2),圆心在直线2x-y-3=0上的圆的方程为( )
| A. | (x-4)2+(y-5)2=10 | B. | (x+4)2+(y-5)2=10 | C. | (x-4)2+(y+5)2=10 | D. | (x+4)2+(y+5)2=10 |
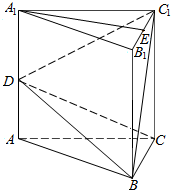 三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=1,AA1=2,点D、E分别为AA1、B1C1的中点.
三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=1,AA1=2,点D、E分别为AA1、B1C1的中点.