题目内容
19.一批产品共10件,其中3件是不合格品,用下列两种不同方式从中随机抽取2件产品检验:方式一:一次性随机抽取2件;
方式二:先随机抽取1件,放回后再随机抽取1件;
记抽取的不合格产品数为ξ.
(1)分别求两种抽取方式下ξ的概率分布;
(2)比较两种抽取方式抽到的不合格品平均数的大小?并说明理由.
分析 (1)方式一中随机变量ξ可取的值为0,1,2,且ξ服从超几何分布ξ~H(2,3,10),计算对应的概率;列出频率分布表;方式二中随机变量ξ可取的值为0,1,2,且ξ服从二项分布ξ~B(2,$\frac{3}{10}$),计算对应的概率;列出频率分布表;
(2)计算方式一与方式二中的数学期望(平均数),比较结果即可.
解答 解:(1)方式一中随机变量ξ可取的值为0,1,2,且ξ服从超几何分布,ξ~H(2,3,10),
于是P(ξ=0)=$\frac{{C}_{3}^{0}{•C}_{7}^{2}}{{C}_{10}^{2}}$=$\frac{7}{15}$;P(ξ=1)=$\frac{{C}_{3}^{1}{•C}_{7}^{1}}{{C}_{10}^{2}}$=$\frac{7}{15}$;P(ξ=2)=$\frac{{C}_{3}^{2}{•C}_{7}^{0}}{{C}_{10}^{2}}$=$\frac{1}{15}$;
因此ξ的频率分布可表示为下表:
| ξ | 0 | 1 | 2 |
| P | $\frac{7}{15}$ | $\frac{7}{15}$ | $\frac{1}{15}$ |
因此ξ的频率分布可表示为下表:
| ξ | 0 | 1 | 2 |
| P | $\frac{49}{100}$ | $\frac{21}{50}$ | $\frac{9}{100}$ |
方式二中ξ的数学期望(平均数)为E(ξ)=2×$\frac{3}{10}$=$\frac{3}{5}$,
所以,两种方式抽到的不合格品平均数相等.
点评 本题考查了离散型随机变量的分布列与数学期望的应用问题,是中档题目.

练习册系列答案
相关题目
8.经过点A(5,2),B(3,2),圆心在直线2x-y-3=0上的圆的方程为( )
| A. | (x-4)2+(y-5)2=10 | B. | (x+4)2+(y-5)2=10 | C. | (x-4)2+(y+5)2=10 | D. | (x+4)2+(y+5)2=10 |
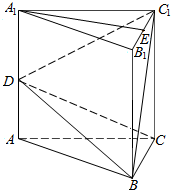 三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=1,AA1=2,点D、E分别为AA1、B1C1的中点.
三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=1,AA1=2,点D、E分别为AA1、B1C1的中点.