题目内容
 已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,
已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,(1)求证四边形EFGH是平行四边形
(2)若AC⊥BD时,求证:EFGH为矩形;
(3)若AC、BD成30°角,AC=6,BD=4,求四边形EFGH的面积;
(4)若AB=BC=CD=DA=AC=BD=2,求AC与BD间的距离.
考点:点、线、面间的距离计算,棱锥的结构特征,直线与平面平行的性质
专题:综合题
分析:(1)根据三角形中位线定理易证EF∥AC,EF=
AC,同理GH∥AC,GH=
AC,所以四边形EFGH是平行四边形
(2)AC⊥BD等价于EF⊥FG,结合(1)可知EFGH为矩形.
(3)由于AC∥EF,BD∥FG,所以得出EF与FG所成的角即为AC、BD所成的角,EFGH中有一内角为30°,利用平行四边形面积公式S=absinθ计算即可.
(4)设M,N分别为BD,AC中点,可以证明MN是BD,AC的公垂线段,在直角三角形AMN中求出MN即可.
| 1 |
| 2 |
| 1 |
| 2 |
(2)AC⊥BD等价于EF⊥FG,结合(1)可知EFGH为矩形.
(3)由于AC∥EF,BD∥FG,所以得出EF与FG所成的角即为AC、BD所成的角,EFGH中有一内角为30°,利用平行四边形面积公式S=absinθ计算即可.
(4)设M,N分别为BD,AC中点,可以证明MN是BD,AC的公垂线段,在直角三角形AMN中求出MN即可.
解答:
解:(1)∵E,F是边AB,BC的中点,∴EF∥AC,EF=
AC,同理GH∥AC,GH=
AC,∴四边形EFGH是平行四边形
(2)∵AC∥EF,BD∥FG,若AC⊥BD,则EF⊥FG,结合(1)可知EFGH为矩形.
(3)∵AC∥EF,BD∥FG,∴EF与FG所成的角即为AC、BD所成的角,∴∠EFG(或其补角)=30°,S EFGH =EF×FG×sin∠EFG=
AC×
BD×sin30°=3
(4)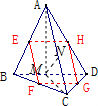 设M,N分别为BD,AC中点,连接MA,MC,MN.则AM⊥BD,CM⊥BD,∴BD⊥面AMC,BD⊆MN,易知AM=CM=
设M,N分别为BD,AC中点,连接MA,MC,MN.则AM⊥BD,CM⊥BD,∴BD⊥面AMC,BD⊆MN,易知AM=CM=
,∴MN⊥AC,∴MN是BD,AC的公垂线段,MN的长即为所求距离.
在直角三角形AMN中,MN=
=
.
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵AC∥EF,BD∥FG,若AC⊥BD,则EF⊥FG,结合(1)可知EFGH为矩形.
(3)∵AC∥EF,BD∥FG,∴EF与FG所成的角即为AC、BD所成的角,∴∠EFG(或其补角)=30°,S EFGH =EF×FG×sin∠EFG=
| 1 |
| 2 |
| 1 |
| 2 |
(4)
 设M,N分别为BD,AC中点,连接MA,MC,MN.则AM⊥BD,CM⊥BD,∴BD⊥面AMC,BD⊆MN,易知AM=CM=
设M,N分别为BD,AC中点,连接MA,MC,MN.则AM⊥BD,CM⊥BD,∴BD⊥面AMC,BD⊆MN,易知AM=CM=| 3 |
在直角三角形AMN中,MN=
| AM2-AN2 |
| 2 |
点评:本题考查空间直线和直线,直线和平面的位置关系的判定,异面直线的夹角和距离求解,考查了空间想象能力、计算能力,分析解决问题能力.空间问题平面化是解决空间几何体问题最主要的思想方法.

练习册系列答案
相关题目
直角坐标平面内,过点P(2,1)且与圆x2+y2=4相切的直线( )
| A、有两条 | B、有且仅有一条 |
| C、不存在 | D、不能确定 |
已知直线z的极坐标方程为ρcos(θ-
) =
,点A的极坐标为(4,
),则点A到直线l的距离为( )
| 3π |
| 4 |
| 2 |
| π |
| 4 |
A、
| ||||
| B、1 | ||||
C、
| ||||
| D、2 |
