题目内容
已知函数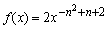 (n∈Z)满足f(8)-f(5)>0.
(n∈Z)满足f(8)-f(5)>0.
(1)求f(x)的解析式;
(2)对于(1)中得到的函数f(x),试判断是否存在k>0,使
h(x)=1-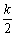 f(x)+(2k―1)x在区间[―1, 2]上的值域为[―4,
f(x)+(2k―1)x在区间[―1, 2]上的值域为[―4,  ]?若存在,求出k;若不存在,请说明理由。
]?若存在,求出k;若不存在,请说明理由。
解:(1)∵f(8)>f(5),即f(x)在第一象限为增函数
∴-n2+n+2>0,得-1<n<2
又由n∈Z,∴n=0或n=1
∴f(x)=2x2
(2)假设存在k>0满足条件,
由已知h(x)=-kx2+(2k-1)x+1,-1≤x≤2
∵h(2)=-1∴两个最值点只能在端点(―1, h(―1))和顶点( ,
, )处取得
)处取得
而 ―h(―1)=
―h(―1)= ―(2―3k)=
―(2―3k)= ≥0
≥0
∴hmax= =
= 且hmin=h(-1)=2-3k=-4
且hmin=h(-1)=2-3k=-4
解得k=2
∴存在k=2满足条件

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 是椭圆
是椭圆 的一个焦点,
的一个焦点, 是短轴的一个端点,线段
是短轴的一个端点,线段 的延长线交
的延长线交 ,且
,且 ,则椭圆
,则椭圆 的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1, 2)在“上”区域内,则双曲线离心率的取值范围为 。
的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1, 2)在“上”区域内,则双曲线离心率的取值范围为 。 的图象大致为
的图象大致为

 B.
B.
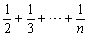 (n∈N*),经计算得f(4)>2, f(8)>
(n∈N*),经计算得f(4)>2, f(8)>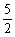 , f(16)>3, f(32)>
, f(16)>3, f(32)> ,
, A.54cm2
A.54cm2  cm2
cm2  =
=  的最大值为( )
的最大值为( ) B.
B.  C. e D.
C. e D. 