题目内容
已知f(n)=1+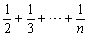 (n∈N*),经计算得f(4)>2, f(8)>
(n∈N*),经计算得f(4)>2, f(8)>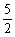 , f(16)>3, f(32)>
, f(16)>3, f(32)> ,
,
……,观察上述结果,则可归纳出一般结论为 。
练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
题目内容
已知f(n)=1+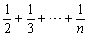 (n∈N*),经计算得f(4)>2, f(8)>
(n∈N*),经计算得f(4)>2, f(8)>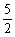 , f(16)>3, f(32)>
, f(16)>3, f(32)> ,
,
……,观察上述结果,则可归纳出一般结论为 。
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案