题目内容
已知A={x||x+1|>0},B={-2,-1,0,1},则(∁RA)∩B=( )
| A、{-1} |
| B、{-2,0,1} |
| C、{0,1} |
| D、{-2} |
考点:交、并、补集的混合运算
专题:集合
分析:根据补集的定义求的∁RA,再根据两个集合的交集的定义求得(∁RA)∩B.
解答:
解:∵A={x||x+1|>0}={x|x≠-1},∴∁RA={-1}.
又∵B={-2,-1,0,1},则(∁RA)∩B={-1},
故选:A.
又∵B={-2,-1,0,1},则(∁RA)∩B={-1},
故选:A.
点评:本题主要考查集合的表示方法、集合的补集,两个集合的交集的定义和求法,属于基础题.

练习册系列答案
相关题目
已知命题p:若
=(1,2)与
=(-2,λ)共线,则λ=-4;命题q:|
|=1,|
|=2,
,
的夹角为
,则|
+
|=
.下面结论正确的是( )
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
| a |
| b |
| 7 |
| A、(¬p)∨q是真命题 |
| B、p∨q是假命题 |
| C、p∧q是假命题 |
| D、p∧(¬q)是真命题 |
已知函数y=sinax+b(a>0)某一个周期的图象如图所示,则函数f(x)=ax2+bx+1零点的个数有( )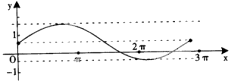

| A、0 | B、1 | C、2 | D、无法确定 |
z=
,则|z|=( )
| 5+12i |
| 3+4i |
A、
| ||
B、
| ||
C、
| ||
D、
|
若实数x,y满足
,则z=x+2y的最小值是( )
|
| A、0 | ||
B、
| ||
| C、5 | ||
| D、1 |
已知O是坐标原点,点A(-1,0),若M(x,y)为平面区域
上的一个动点,则|
+
|的最小值是( )
|
| OA |
| OM |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
设复数ω=-
+
i(i为虚数单位),则(ω+1)2=( )
| 1 |
| 2 |
| ||
| 2 |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
各大学在高考录取时采取专业志愿优先的录取原则.一考生从某大学所给的7个专业中,选择3个作为自己的第一、二、三专业志愿,其中甲、乙两个专业不能同时兼报,则该考生不同的填报专业志愿的方法有( )
| A、210种 | B、180种 |
| C、120种 | D、95种 |