题目内容
已知O是坐标原点,点A(-1,0),若M(x,y)为平面区域
上的一个动点,则|
+
|的最小值是( )
|
| OA |
| OM |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
考点:简单线性规划
专题:数形结合
分析:由题意作出可行域,由向量的坐标加法运算求得
+
的坐标,把|
+
|转化为可行域内的点M(x,y)到定点N(1,0)的距离,数形结合可得答案.
| OA |
| OM |
| OA |
| OM |
解答:
解:由约束条件
作平面区域如图,
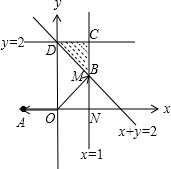
∵A(-1,0),M(x,y),
∴
+
=(-1,0)+(x,y)=(x-1,y),
则|
+
|=
.
要使|
+
|最小,则可行域内的点M(x,y)到定点N(1,0)的距离最小.
由图可知,当M与B重合时满足题意.
联立
,得B(1,1).
∴|
+
|的最小值是1.
故选:B.
|

∵A(-1,0),M(x,y),
∴
| OA |
| OM |
则|
| OA |
| OM |
| (x-1)2+y2 |
要使|
| OA |
| OM |
由图可知,当M与B重合时满足题意.
联立
|
∴|
| OA |
| OM |
故选:B.
点评:本题考查了简单的线性规划,考查了数形结合、转化与化归等解题思想方法,考查了向量模的求法,是中档题.

练习册系列答案
相关题目
如果复数(m-i)i(其中m∈R)的实部与虚部互为相反数,则m=( )
| A、2 | B、-2 | C、-1 | D、1 |
已知点F(
,0),A(-1,0),B(1,0),直线x=
上有两个动点M,N,始终使∠MFN=45°,三角形MFN的外心轨迹为曲线C,P为曲线C在一象限内的动点,设∠PAB=α,∠PBA=β,∠APB=γ,则( )
| 2 |
| ||
| 2 |
| A、tanα+tanβ+tanγ=0 |
| B、tanα+tanβ-tanγ=0 |
| C、tanα+tanβ+2tanγ=0 |
| D、tanα+tanβ-2tanγ=0 |
如图是某算法的程序框图,当输出的结果T>100时,整数s的最小值是( )


| A、2 | B、3 | C、4 | D、5 |
已知A={x||x+1|>0},B={-2,-1,0,1},则(∁RA)∩B=( )
| A、{-1} |
| B、{-2,0,1} |
| C、{0,1} |
| D、{-2} |
已知集合M={y|y=2cosx}.N={x|
≤0}.则集合M∩N=( )
| x+1 |
| x-2 |
| A、{x|-2≤x≤-1} |
| B、{x|-1≤x≤2} |
| C、{x|-1≤x<2} |
| D、{x|-1<x≤2} |
已知复数z满足z(1+i)=1(其中i为虚数单位).则z的共轭复数
所对应的点位于( )
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知θ为锐角,sinθ=
,则sin(θ+
)等于( )
| ||
| 5 |
| π |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|