题目内容
 如图,正三棱柱ABC-A1B1C1中,底面边长为2,侧棱长为
如图,正三棱柱ABC-A1B1C1中,底面边长为2,侧棱长为| 2 |
(1)求证:BC1∥平面AB1D;
(2)求二面角A1-AB1-D的大小.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:计算题,证明题,空间位置关系与距离,空间角
分析:(1)连接A1B与AB1交于E,则E为A1B的中点,D为A1C1的中点,根据中位线可知BC1∥DE,又DE?平面AB1D,BC1?平面AB1D,根据线面平行的判定定理可知BC1∥平面AB1D;
(2)过D作DF⊥A1B1于F,由正三棱柱的性质可知,DF⊥平面AB1,连接EF,DE,在正△A1B1C1中,求出B1D,在直角三角形AA1D中,求出AD,即可证得AD=B1D,则DE⊥AB1,由三垂线定理的逆定理可得EF⊥AB1.则∠DEF为二面角A1-AB1-D的平面角,根据△B1FE∽△B1AA1,即可求出∠DEF.
(2)过D作DF⊥A1B1于F,由正三棱柱的性质可知,DF⊥平面AB1,连接EF,DE,在正△A1B1C1中,求出B1D,在直角三角形AA1D中,求出AD,即可证得AD=B1D,则DE⊥AB1,由三垂线定理的逆定理可得EF⊥AB1.则∠DEF为二面角A1-AB1-D的平面角,根据△B1FE∽△B1AA1,即可求出∠DEF.
解答:
解:(1)连接A1B与AB1交于E,则E为A1B的中点,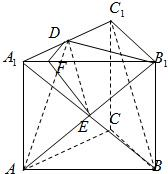
∵D为A1C1的中点,
∴DE为△A1BC1的中位线,
∴BC1∥DE.
又DE?平面AB1D,BC1?平面AB1D,
∴BC1∥平面AB1D
(2)过D作DF⊥A1B1于F,由正三棱柱的性质可知,DF⊥平面AB1,
连接EF,DE,在正△A1B1C1中,
∴B1D=
A1B1=
,
在直角三角形AA1D中,∵AD=
=
,
∴AD=B1D.
∴DE⊥AB1,
由三垂线定理的逆定理可得EF⊥AB1.
则∠DEF为二面角A1-AB1-D的平面角,又得DF=
,
∵△B1FE∽△B1AA1,
∴
=
,则EF=
,
∴∠DEF=
.
故所求二面角A1-AB1-D的大小为
.

∵D为A1C1的中点,
∴DE为△A1BC1的中位线,
∴BC1∥DE.
又DE?平面AB1D,BC1?平面AB1D,
∴BC1∥平面AB1D
(2)过D作DF⊥A1B1于F,由正三棱柱的性质可知,DF⊥平面AB1,
连接EF,DE,在正△A1B1C1中,
∴B1D=
| ||
| 2 |
| 3 |
在直角三角形AA1D中,∵AD=
| AA12+A1D2 |
| 3 |
∴AD=B1D.
∴DE⊥AB1,
由三垂线定理的逆定理可得EF⊥AB1.
则∠DEF为二面角A1-AB1-D的平面角,又得DF=
| ||
| 2 |
∵△B1FE∽△B1AA1,
∴
| EF |
| AA1 |
| B1E |
| A1B1 |
| ||
| 2 |
∴∠DEF=
| π |
| 4 |
故所求二面角A1-AB1-D的大小为
| π |
| 4 |
点评:本题主要考查直线与平面平行的判定,以及平面与平面垂直的判定等有关知识,二面角的求解在最近两年高考中频繁出现,值得重视.

练习册系列答案
相关题目
0<α<π,且sin(α+
)=-
,则tan2α等于( )
| π |
| 4 |
| ||
| 10 |
A、
| ||
B、-
| ||
C、±
| ||
D、
|
设全集U=R,对R的任意子集A、B,记A⊕B={x|x∈A∪B,且x∉A∩B},若R的子集X、Y、Z满足X⊕Y=X⊕Z.则Y与Z的关系是( )
| A、Y=Z | B、Y∩Z=∅ |
| C、Y∪Z=R | D、不能确定 |