题目内容
6．sin（-$\frac{10π}{3}$）的值是（ ）| A． | -$\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
分析 由条件利用诱导公式进行化简所给的式子，可得结果．
解答 解：sin（-$\frac{10π}{3}$）=sin（-4π+$\frac{2π}{3}$）=sin$\frac{2π}{3}$=sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$，
故选：B．
点评 本题主要考查应用诱导公式化简三角函数式，要特别注意符号的选取，这是解题的易错点，属于基础题．
练习册系列答案
相关题目
17．下列函数中，在其定义域内是增函数而且又是奇函数的是（ ）
| A． | $y=x+\frac{1}{x}$ | B． | y=2x-2-x | C． | y=log2|x| | D． | y=2x+2-x |
14．已知$sinα-2cosα=\frac{{\sqrt{10}}}{2}$，则tan2α=（ ）
| A． | $\frac{4}{3}$ | B． | $-\frac{3}{4}$ | C． | $\frac{3}{4}$ | D． | $-\frac{4}{3}$ |
1．双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{16}$=1的离心率是（ ）
| A． | $\frac{3}{5}$ | B． | $\frac{5}{3}$ | C． | $\frac{\sqrt{41}}{5}$ | D． | $\frac{5}{\sqrt{41}}$ |
15．下列命题中错误的是（ ）
| A． | 如果平面α⊥平面γ，平面β⊥平面γ，α∩β=l，那么l⊥γ | |
| B． | 如果平面α⊥平面β，那么平面α内一定存在直线平行于平面β | |
| C． | 如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β | |
| D． | 如果平面α⊥平面β，α∩β=l，过α内任意一点作l的垂线m，则m⊥β |
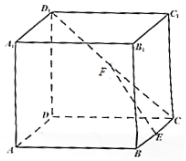如图，在正方体ABCD-A1B1C1D1中，E、F分别是线段BC、CD1的中点．