题目内容
2.为了调整个人所得税征收制度,某机构准备调查了解某市市民的收人情况,随机抽取了n名市民进行试点凋查,其月收人介于1200元和4200元之间,将调查结果按如下方式分为五组:第一组[1200,1800):第二组[1800,2400)…:第五组[3600,4200].下表是按上述分组方式得到的频率分布表:| 分组 | 频数 | 频率 |
| [1200,1800) | x | A |
| [1800,2400) | 90 | B |
| [2400,3000) | y | 0.40 |
| [3000,3600) | 160 | 0.32 |
| [3600,4200] | z | 0.04 |
(Ⅱ)为了了解市民对个人所得税征收制度的意见,现利用分层抽样的方法从这n名市民中抽取一个容量为50的样本进行问卷凋查,若从第一组或第五组中抽取的市民中任选两名,求事件“两人收入之差大于1000元”的概率.
分析 (Ⅰ)由表中条件利用频率=$\frac{频数}{总数}$,能求出x,y,z,a,b的值.
(Ⅱ)由题意先求出分层抽样比,从而得到在样本中第一组抽出3人,第五组抽出2人,从这五人中任取两人,基本事件总数n=${C}_{5}^{2}$=10,事件“两人收入之差大于1000元”是指在第一组和第五组中各取一人,求出其包含怕基本事件个数,由此能求出事件“两人收入之差大于1000元”的概率.
解答 解:(Ⅰ)由表知:$n=\frac{160}{0.32}$=500,b=$\frac{90}{500}=0.18$,
y=500×0.40=200,z=500×0.04=20,
x=500-90-200-160-20=30,a=$\frac{30}{500}=0.06$.
(Ⅱ)由题意知分层抽样比为$\frac{50}{500}=\frac{1}{10}$,
∴在样本中第一组抽出的人数为30×$\frac{1}{10}$=3,
第五组抽出的人数为20×$\frac{1}{10}$=2,
从这五人中任取两人,基本事件总数n=${C}_{5}^{2}$=10,
事件“两人收入之差大于1000元”是指在第一组和第五组中各取一人,
包含怕基本事件个数m=${C}_{3}^{1}{C}_{2}^{1}=6$,
∴事件“两人收入之差大于1000元”的概率:p=$\frac{6}{10}=\frac{3}{5}$.
点评 本题考查频率分布表的应用,考查概率的求法,是基础题,解题时要认真审题,注意分层抽样、等可能事件概率计算公式的合理运用.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
13.已知tanα=2,则$\frac{sinα+2cosα}{sinα-cosα}$=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
7.下列关于函数f(x)=sinx(cosx+sinx)的说法中,不正确的是( )
| A. | f(x)的最小正周期为π | |
| B. | f(x)的图象关于直线x=-$\frac{π}{8}$对称 | |
| C. | f(x)的图象关于点($\frac{π}{8}$,0)对称 | |
| D. | f(x)的图象向右平移$\frac{π}{8}$后得到一个偶函数的图象 |
11.已知关于x的二次函数f(x)=ax2-4bx+1,设集合A={-1,1,2,3,4,5},B={-2,-1,1,2,3,4},分别从集合A和B中随机取一个数记为a和b,则函数y=f(x)在[1,+∞)上单调递增的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{9}$ |
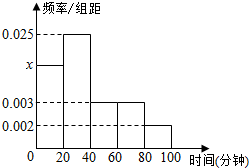 某中学随机抽取50名高一学生调查其每天运动的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,运动
某中学随机抽取50名高一学生调查其每天运动的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,运动