题目内容
11.已知关于x的二次函数f(x)=ax2-4bx+1,设集合A={-1,1,2,3,4,5},B={-2,-1,1,2,3,4},分别从集合A和B中随机取一个数记为a和b,则函数y=f(x)在[1,+∞)上单调递增的概率为( )| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{9}$ |
分析 要使函数f(x)=ax2-4bx+1在区间[1,+∞)上为增函数,当且仅当a>0且$\frac{2b}{a}$≤1,即2b≤a,由此利用列举法能求出函数y=f(x)在[1,+∞)上单调递增的概率.
解答 解:∵函数f(x)=ax2-4bx+1的图象的对称轴为x=$\frac{2b}{a}$,
要使函数f(x)=ax2-4bx+1在区间[1,+∞)上为增函数,
当且仅当a>0且$\frac{2b}{a}$≤1,即2b≤a,
若a=1,则b=-2,-1;
若a=2,则b=-2,-1,1;
若a=3,则b=-2,-1,1;
若a=4,则b=-2,-1,1,2;
若a=5,则b=-2,-1,1,2;
∴所求事件包含基本事件的个数是2+3+3+4+4=16,
∴所求事件的概率为$\frac{16}{36}$=$\frac{4}{9}$.
故选:D.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
2.为了调整个人所得税征收制度,某机构准备调查了解某市市民的收人情况,随机抽取了n名市民进行试点凋查,其月收人介于1200元和4200元之间,将调查结果按如下方式分为五组:第一组[1200,1800):第二组[1800,2400)…:第五组[3600,4200].下表是按上述分组方式得到的频率分布表:
(I)求n及上表中的x,y,z,a,b的值;
(Ⅱ)为了了解市民对个人所得税征收制度的意见,现利用分层抽样的方法从这n名市民中抽取一个容量为50的样本进行问卷凋查,若从第一组或第五组中抽取的市民中任选两名,求事件“两人收入之差大于1000元”的概率.
| 分组 | 频数 | 频率 |
| [1200,1800) | x | A |
| [1800,2400) | 90 | B |
| [2400,3000) | y | 0.40 |
| [3000,3600) | 160 | 0.32 |
| [3600,4200] | z | 0.04 |
(Ⅱ)为了了解市民对个人所得税征收制度的意见,现利用分层抽样的方法从这n名市民中抽取一个容量为50的样本进行问卷凋查,若从第一组或第五组中抽取的市民中任选两名,求事件“两人收入之差大于1000元”的概率.
6.已知p:0<a<4,q:函数y=x2-ax+a的值恒为正,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.已知点A(2,0),B(0,3),则直线AB的方程为( )
| A. | 3x-2y-6=0 | B. | 2x-3y+6=0 | C. | 3x+2y-6=0 | D. | 2x+3y+6=0 |
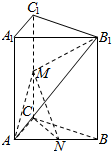 如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC=BC,M,N分别是棱CC1,AB的中点.
如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC=BC,M,N分别是棱CC1,AB的中点.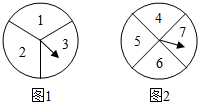 某校高一年级甲、已两班准备联合举行晚会,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.甲班的文娱委员利用分别标有数字1,2,3,4,5,6,7的两个转盘(如图所示),设计了一种游戏方案:两人同时各转动一个转盘一次,将转到的数字相加,和为偶数时甲班代表获胜,否则乙班代表获胜.
某校高一年级甲、已两班准备联合举行晚会,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.甲班的文娱委员利用分别标有数字1,2,3,4,5,6,7的两个转盘(如图所示),设计了一种游戏方案:两人同时各转动一个转盘一次,将转到的数字相加,和为偶数时甲班代表获胜,否则乙班代表获胜.