题目内容
在△ABC中,若lg(a+c)+lg(a-c)=lg b-lg  ,则A等于( )
,则A等于( )
(A) (B)
(B) (C)
(C) (D)
(D)
C解析:由lg(a+c)+lg(a-c)=lg b-lg  ,
,
整理得,
lg(a+c)·(a-c)=lg b(b+c),
∴(a+c)·(a-c)=b(b+c),
得b2+c2-a2=-bc.
∴cos A= =-
=- ,
,
又A∈(0,π),
∴A= .故选C.
.故选C.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 tan α的值为 .
tan α的值为 . 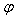 )(ω>0,-
)(ω>0,- ≤
≤ 个单位长度得到y=sin x的图象,则f(
个单位长度得到y=sin x的图象,则f( ,cos β=
,cos β= ),则α+β= .
),则α+β= .  sin xcos x-2sin2x+1.
sin xcos x-2sin2x+1. )的值;
)的值;
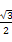 accos B.
accos B. ≤A≤
≤A≤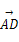 =(3,7),
=(3,7),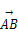 =(-2,3),对角线AC与BD交于点O,则
=(-2,3),对角线AC与BD交于点O,则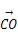 的坐标为( )
的坐标为( ) ,5) (B)(
,5) (B)( =16,|
=16,| +
+ |=|
|=| |= ( ).
|= ( ).