题目内容
已知函数f（x）=2sin（x-
）cosx+sinxcosx+
sin2x（x∈R）．
（1）求f（x）的单调递增区间；
（2）在△ABC中，B为锐角，且f（B）=
，AC=4
，D是BC边上一点，AB=AD，试求AD+DC的最大值．
| π |
| 3 |
| 3 |
（1）求f（x）的单调递增区间；
（2）在△ABC中，B为锐角，且f（B）=
| 3 |
| 3 |
考点：两角和与差的正弦函数,二倍角的正弦,正弦函数的单调性,正弦定理
专题：三角函数的求值,三角函数的图像与性质
分析：（1）利用两角和差的正弦公式、倍角公式、正弦函数的单调性即可得出；
（2）利用（1）的结论可得B，得出三角形为等边三角形，再利用正弦定理即可得出．
（2）利用（1）的结论可得B，得出三角形为等边三角形，再利用正弦定理即可得出．
解答：
解：（1）f(x)=2(
sinx-
cosx)cosx+sinxcosx+
sin2x
=2sinxcosx-
(cos2x-sin2x)
=sin2x-
cos2x
=2sin(2x-
)．
由-
+2kπ≤2x-
≤
+2kπ，得-
+kπ≤x≤
+kπ（k∈Z）．
（2）由f(B)=
得sin(2B-
)=
．
又0＜B＜
，则-
＜2B-
＜
，从而2B-
=
，∴B=
．
由AB=AD知△ABD是正三角形，AB=AD=BD，
∴AD+DC=BD+DC=BC，
在△ABC中，由正弦定理，得
=
，即BC=8sin∠BAC．
∵D是BC边上一点，∴
＜∠BAC＜
，∴
＜sin∠BAC≤1，知4
＜BC≤8．
当∠BAC=
，C=
时，AD+CD取得最大值8．
| 1 |
| 2 |
| ||
| 2 |
| 3 |
=2sinxcosx-
| 3 |
=sin2x-
| 3 |
=2sin(2x-
| π |
| 3 |
由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
（2）由f(B)=
| 3 |
| π |
| 3 |
| ||
| 2 |
又0＜B＜
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
由AB=AD知△ABD是正三角形，AB=AD=BD，
∴AD+DC=BD+DC=BC，
在△ABC中，由正弦定理，得
4
| ||
sin
|
| BC |
| sin∠BAC |
∵D是BC边上一点，∴
| π |
| 3 |
| 2π |
| 3 |
| ||
| 2 |
| 3 |
当∠BAC=
| π |
| 2 |
| π |
| 6 |
点评：本题考查了两角和差的正弦公式、倍角公式、正弦函数的单调性、等边三角形的性质、正弦定理，考查了推理能力和计算能力，属于难题．
练习册系列答案
相关题目
如图，圆柱内有一个三棱柱，三棱柱的底面在圆柱底面内，并且底面是正三角形，如果圆柱的体积是16π，底面直径与母线长相等．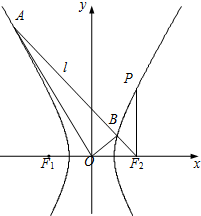
设点P在以F1、F2为左、右焦点的双曲线C：