题目内容
10.设Sn是数列{an}的前n项和,an>0,且${S_n}=\frac{1}{6}{a_n}({a_n}+3)$.(1)求数列{an}的通项公式;
(2)设${b_n}=\frac{1}{{({a_n}-1)({a_n}+2)}}$,Tn=b1+b2+…+bn,求证:${T_n}<\frac{1}{6}$.
分析 (1)通过${S_n}=\frac{1}{6}{a_n}({a_n}+3)$与Sn-1=$\frac{1}{6}$an-1(an-1+3)作差,进而可知数列{an}是首项、公差均为3的等差数列,计算即得结论;
(2)通过(1)裂项可知bn=$\frac{1}{3}$($\frac{1}{3n-1}$-$\frac{1}{3n+2}$),进而并项相加即得结论.
解答 (1)解:∵${S_n}=\frac{1}{6}{a_n}({a_n}+3)$,Sn-1=$\frac{1}{6}$an-1(an-1+3),
∴an=$\frac{1}{6}$[${{a}_{n}}^{2}$+3an-(${{a}_{n-1}}^{2}$+3an-1)],
整理得:${{a}_{n}}^{2}$-${{a}_{n-1}}^{2}$=3(an+an-1),
又∵an>0,
∴an-an-1=3,
又∵a1=$\frac{1}{6}$a1(a1+3),即a1=3或a1=0(舍),
∴数列{an}是首项、公差均为3的等差数列,
∴其通项公式an=3n;
(2)证明:由(1)可知${b_n}=\frac{1}{{({a_n}-1)({a_n}+2)}}$=$\frac{1}{(3n-1)(3n+2)}$=$\frac{1}{3}$($\frac{1}{3n-1}$-$\frac{1}{3n+2}$),
∴Tn=b1+b2+…+bn
=$\frac{1}{3}$($\frac{1}{2}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{8}$+…+$\frac{1}{3n-1}$-$\frac{1}{3n+2}$)
=$\frac{1}{3}$($\frac{1}{2}$-$\frac{1}{3n+2}$)
<$\frac{1}{6}$.
点评 本题考查数列的通项及前n项和,考查裂项相消法,注意解题方法的积累,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{2015}{2016}$ | B. | $\frac{4028}{2015}$ | C. | $\frac{4032}{2017}$ | D. | $\frac{2014}{2015}$ |
| A. | (1,1+$\sqrt{2}$) | B. | ($\sqrt{2}$,1+$\sqrt{2}$) | C. | (1+$\sqrt{2}$,1+$\sqrt{3}$) | D. | (1+$\sqrt{2}$,+∞) |

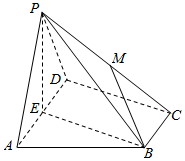 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,$BC=\frac{1}{2}AD=1$,$CD=\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,$BC=\frac{1}{2}AD=1$,$CD=\sqrt{3}$.