题目内容
12.已知$\frac{π}{2}<α<π$,3sin2α=2cosα,则$sin(α-\frac{9π}{2})$=$\frac{2\sqrt{2}}{3}$.分析 $\frac{π}{2}<α<π$,可得cosα<0,由3sin2α=2cosα,即6sinαcosα=2cosα,可得sinα=$\frac{1}{3}$再利用诱导公式与平方关系即可得出.
解答 解:∵$\frac{π}{2}<α<π$,∴cosα<0.
∵3sin2α=2cosα,即6sinαcosα=2cosα,∴sinα=$\frac{1}{3}$,
则$sin(α-\frac{9π}{2})$=-cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{2\sqrt{2}}{3}$.
故答案为:$\frac{{2\sqrt{2}}}{3}$.
点评 本题考查了三角函数基本关系式、倍角公式、诱导公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
17.已知平面向量$\vec a,\vec b$的夹角为$60°,\vec a=({\sqrt{3},1}),|\vec b|=1$则$|\vec a+2\vec b|$=( )
| A. | 2 | B. | $\sqrt{7}$ | C. | $2\sqrt{7}$ | D. | $2\sqrt{3}$ |
1.已知正方形ABCD的边长为2,E为CD的中点,则$\overrightarrow{AE}•\overrightarrow{CB}$=( )
| A. | -4 | B. | -3 | C. | 4 | D. | $2\sqrt{5}$ |
13.以F(0,1)为焦点的抛物线的标准方程是( )
| A. | x2=4y | B. | x2=2y | C. | y2=4x | D. | y2=2x |
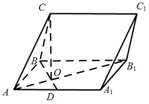 在三棱柱ABCA1B1C1中,侧面ABB1A1为矩形,AB=3,AA1=3$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
在三棱柱ABCA1B1C1中,侧面ABB1A1为矩形,AB=3,AA1=3$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
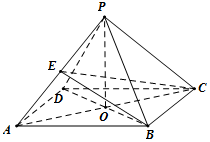 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,AC∩BD=O.
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,AC∩BD=O.