题目内容
3.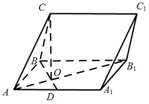 在三棱柱ABCA1B1C1中,侧面ABB1A1为矩形,AB=3,AA1=3$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
在三棱柱ABCA1B1C1中,侧面ABB1A1为矩形,AB=3,AA1=3$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.(Ⅰ)证明:BC⊥AB1;
(Ⅱ)若OC=OA,求二面角A1-AC-B的余弦值.
分析 (Ⅰ)由题意求得∠ABD=∠AB1B,且∠ABD+∠BAB1=∠AB1B+∠BAB1=$\frac{π}{2}$,则AB1⊥BD.再由CO⊥侧面ABB1A1,得AB1⊥CO.结合线面垂直的判定可得AB1⊥平面CBD,进一步得到BC⊥AB1;
(Ⅱ)以O为原点,分别以OD,OB1,OC所在的直线为x,y,z轴,建立空间直角坐标系Oxyz,求出相应点的坐标,再求得平面ABC及平面A1AC的法向量,由两个法向量所成角的余弦值可得二面角A1-AC-B的平面角的余弦值.
解答 (Ⅰ)证明:由题意tan∠ABD=$\frac{AD}{AB}$=$\frac{\sqrt{2}}{2}$,tan∠AB1B=$\frac{AB}{BB1}$=$\frac{\sqrt{2}}{2}$,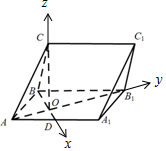
∵0<∠ABD<$\frac{π}{2}$,0<∠AB1B<$\frac{π}{2}$,∴∠ABD=∠AB1B,
∴∠ABD+∠BAB1=∠AB1B+∠BAB1=$\frac{π}{2}$,则AB1⊥BD.
又CO⊥侧面ABB1A1,AB1⊥CO.
又BD与CO交于点O,AB1⊥平面CBD,
又BC?平面CBD,BC⊥AB1;
(Ⅱ)解:如图,以O为原点,分别以OD,OB1,OC所在的直线为x,y,z轴,建立空间直角坐标系Oxyz,
则$A(0,-\sqrt{3},0)$,B($-\sqrt{6}$,0,0),C(0,0,$\sqrt{3}$),B1($0,2\sqrt{3},0$),
∴$\overrightarrow{AB}=(-\sqrt{6},\sqrt{3},0)$,$\overrightarrow{AC}=(0,\sqrt{3},\sqrt{3})$,$\overrightarrow{A{A}_{1}}=\overrightarrow{B{B}_{1}}=(\sqrt{6},2\sqrt{3},0)$.
设平面ABC的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=-\sqrt{6}x+\sqrt{3}y=0}\\{\overrightarrow{n}•\overrightarrow{AC}=\sqrt{3}y+\sqrt{3}z=0}\end{array}\right.$,令x=1,可得$\overrightarrow{n}$=(1,$\sqrt{2}$,-$\sqrt{2}$)是平面ABC的一个法向量.
设平面A1AC的法向量为$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{A{A}_{1}}=\sqrt{6}x+2\sqrt{3}y=0}\\{\overrightarrow{m}•\overrightarrow{AC}=\sqrt{3}y+\sqrt{3}z=0}\end{array}\right.$,令x=2,可得$\overrightarrow{m}$=(2,-$\sqrt{2}$,$\sqrt{2}$)是平面A1AC的一个法向量.
设二面角A1-AC-B的平面角为α,则cosα=|cos<$\overrightarrow{m},\overrightarrow{n}$>|=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$|=$\frac{2}{2\sqrt{2}×\sqrt{5}}$=$\frac{\sqrt{10}}{10}$.
二面角A1-AC-B的余弦值为$\frac{\sqrt{10}}{10}$.
点评 本题考查空间中直线与直线的位置关系,考查二面角平面角的求法,训练了利用空间向量求解二面角的平面角,是中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 向右平移$\frac{π}{4}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向左平移$\frac{π}{12}$个单位长度 |
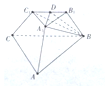 已知三棱台ABC-A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6
已知三棱台ABC-A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6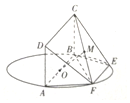 如图,AB为圆O的直径,点E,F在圆O上,AB∥EF,矩形ABCD所在的平面和圆(x-1)2+y2=1所在的平面互相垂直,且AB=2,AD=EF=1,∠BAF=60°.
如图,AB为圆O的直径,点E,F在圆O上,AB∥EF,矩形ABCD所在的平面和圆(x-1)2+y2=1所在的平面互相垂直,且AB=2,AD=EF=1,∠BAF=60°.