题目内容
17.已知平面向量$\vec a,\vec b$的夹角为$60°,\vec a=({\sqrt{3},1}),|\vec b|=1$则$|\vec a+2\vec b|$=( )| A. | 2 | B. | $\sqrt{7}$ | C. | $2\sqrt{7}$ | D. | $2\sqrt{3}$ |
分析 由向量$\overrightarrow{a}$的坐标求得$|\overrightarrow{a}|$,再由向量的数量积的定义求出$\overrightarrow{a}•\overrightarrow{b}$的值,再根根 $|\vec a+2\vec b|$=$\sqrt{(\overrightarrow{a}+2\overrightarrow{b})^{2}}=\sqrt{{\overrightarrow{a}}^{2}+4\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}}$求出结果.
解答 解:∵$\overrightarrow{a}=(\sqrt{3},1)$,∴$|\overrightarrow{a}|=2$,
又平面向量$\vec a,\vec b$的夹角为60°,|b|=1,
∴$\overrightarrow{a}•\overrightarrow{b}$=2×1×cos60°=1,
∴$|\vec a+2\vec b|$=$\sqrt{(\overrightarrow{a}+2\overrightarrow{b})^{2}}=\sqrt{{\overrightarrow{a}}^{2}+4\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}}$=2$\sqrt{3}$.
故选:D.
点评 本题主要考查两个向量的数量积的定义,求向量的模的方法,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.为了调查黄山市某校高中学生是否愿意在寒假期间参加志愿者活动,用简单随机抽样方法从该校调查了80人,结果如下:
(1)若用分层抽样的方法在愿意参加志愿者活动的学生抽取5人,则应女生中抽取多少人?
(2)在(1)中抽取出的5人中任选2人,求“被选中的恰好是一男一女”的概率.
注:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 是否愿意提供志愿者服务 性别 | 愿意 | 不愿意 |
| 男生 | 30 | 10 |
| 女生 | 20 | 20 |
(2)在(1)中抽取出的5人中任选2人,求“被选中的恰好是一男一女”的概率.
| P(K2≥k0) | 0.025 | 0.010 |
| k0 | 5.024 | 6.635 |
9.已知0<a<b,且a+b=1,则下列不等式中正确的是( )
| A. | log2a>0 | B. | 2a-b<$\frac{1}{2}$ | C. | log2a+log2b<-2 | D. | 2($\frac{a}{b}$+$\frac{b}{a}$)<$\frac{1}{2}$ |
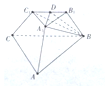 已知三棱台ABC-A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6
已知三棱台ABC-A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6