题目内容
7.已知函数f(x)=|4x-a|+|4x+3|,g(x)=|x-1|-|2x|.(1)解不等式g(x)>-3;
(2)若存在x1∈R,也存在x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.
分析 (1)通过讨论x的范围求出各个区间上的不等式的解集,取并集即可;
(2)因为存在x1∈R,存在x2∈R,使得f(x1)=g(x2)成立,所以{y|y=f(x),x∈R}∩{y|y=g(x),x∈R}≠∅,分别求出f(x),g(x)的范围,即可求实数a的取值范围.
解答 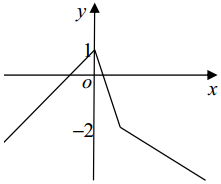 解:(1)由题意可得$g(x)=\left\{\begin{array}{l}1+x,x≤0\\ 1-3x,0<x<1\\-1-x,x≥1\end{array}\right.$
解:(1)由题意可得$g(x)=\left\{\begin{array}{l}1+x,x≤0\\ 1-3x,0<x<1\\-1-x,x≥1\end{array}\right.$
因为g(x)>-3,
由函数图象可得不等式的解为-4<x<2,
所以不等式的解集为{x|-4<x<2}.
(2)因为存在x1∈R,存在x2∈R,使得f(x1)=g(x2)成立,
所以{y|y=f(x),x∈R}∩{y|y=g(x),x∈R}≠∅,
又f(x)=|4x-a|+|4x+3|≥|(4x-a)+(4x+3)|=|a+3|,
由(1)可知g(x)max=1,所以|a+3|≤1,解得-4≤a≤-2,
所以实数a的取值范围为[-4,-2].
点评 本题考查了解绝对值不等式问题,考查集合的包含关系,是一道中档题.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
17.为了调查黄山市某校高中部学生是否愿意在寒假期间参加志愿者活动,现用简单随机抽样方法,从该校高中部抽取男生和女生共60人进行问卷调查,问卷结果统计如下:
(1)若用分层抽样的方法在愿意参加志愿者活动的学生抽取8人,则应从愿意参加志愿者活动的女生中抽取多少人?
(2)在(1)中抽取出的8人中任选3人,求被抽中的女生人数的分布列和数学期望.
| 是否愿意提供志愿者服务 性别 | 愿意 | 不愿意 |
| 男生 | 25 | 5 |
| 女生 | 15 | 15 |
(2)在(1)中抽取出的8人中任选3人,求被抽中的女生人数的分布列和数学期望.
2.大数据时代出现了滴滴打车服务,二胎政策的放开使得家庭中有两个小孩的现象普遍存在,某城市关系要好的A,B,C,D四个家庭各有两个小孩共8人,准备使用滴滴打车软件,分乘甲、乙两辆汽车出去游玩,每车限坐4名(乘同一辆车的4名小孩不考虑位置),其中A户家庭的孪生姐妹需乘同一辆车,则乘坐甲车的4名小孩恰有2名来自于同一个家庭的乘坐方式共有( )
| A. | 18种 | B. | 24种 | C. | 36种 | D. | 48种 |
19.已知函数F(x)=xf(x),f(x)满足f(x)=f(-x),且当x∈(-∞,0]时,F'(x)<0成立,若$a={2^{0.1}}•f({{2^{0.1}}}),b=ln2•f({ln2}),c={log_2}\frac{1}{8}•f({{{log}_2}\frac{1}{8}})$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | c>a>b | C. | c>b>a | D. | a>c>b |
8.若集合A={x|x2<4},且A∪B=A,则集合B可能是( )
| A. | {1,2} | B. | {x|x<2} | C. | {-1,0,1} | D. | R |
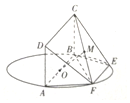 如图,AB为圆O的直径,点E,F在圆O上,AB∥EF,矩形ABCD所在的平面和圆(x-1)2+y2=1所在的平面互相垂直,且AB=2,AD=EF=1,∠BAF=60°.
如图,AB为圆O的直径,点E,F在圆O上,AB∥EF,矩形ABCD所在的平面和圆(x-1)2+y2=1所在的平面互相垂直,且AB=2,AD=EF=1,∠BAF=60°.