题目内容
已知a，b，c∈R，a+b+c=0，abc＞0，T=
+
+
，则（ ）
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| A、T＞0 | B、T＜0 |
| C、T=0 | D、T≥0 |
考点：不等式的基本性质
专题：不等式的解法及应用
分析：由a+b+c=0，abc＞0，可知：三个数中一正两负，不妨设a＞0，b＜0，c＜0．通过化简利用不等式的性质即可得出．
解答：
解：由a+b+c=0，abc＞0，
可知：三个数中一正两负，不妨设a＞0，b＜0，c＜0．
则T=
+
+
=
=
=
，
∵ab＜0，-c2＜0，abc＞0，
∴T＜0．
故选：B．
可知：三个数中一正两负，不妨设a＞0，b＜0，c＜0．
则T=
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| bc+ac+ab |
| abc |
| ab+c(a+b) |
| abc |
| ab-c2 |
| abc |
∵ab＜0，-c2＜0，abc＞0，
∴T＜0．
故选：B．
点评：本题考查了不等式的性质，属于基础题．
练习册系列答案
全优点练单元计划系列答案
相关题目
已知函数f（x）=x+cosx，则f′（
）=（ ）
| π |
| 6 |
A、
| ||||
B、
| ||||
C、1-
| ||||
D、
|
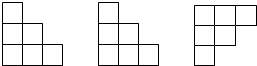已知若干个正方体小木块堆放在一起形成的组合体的三视图如图所示，则所需小木块最少有多少个（ ）| A、7个 | B、8个 | C、9个 | D、10个 |
函数f（x）=（x-2）ln（x2-4x+4）-（x-2）ln4的零点个数为（ ）
| A、3 | B、2 | C、1 | D、0 |
对于实数a和b，定义运算a*b，运算原理如图所示，则式子(| 1 |
| 4 |
| 1 |
| 2 |
| A、6 | B、7 | C、8 | D、9 |
给出以下命题：
①?x∈R，sinx+cosx＞1；
②?x∈R，x2-x+1＜0；
③“x＞1”是“|x|＞1”的充分不必要条件；
④若
•
=0，则|
|=|
|=0．
其中假命题的个数是（ ）
①?x∈R，sinx+cosx＞1；
②?x∈R，x2-x+1＜0；
③“x＞1”是“|x|＞1”的充分不必要条件；
④若
| a |
| b |
| a |
| b |
其中假命题的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
已知函数f（x）=
，则f（2）=（ ）
|
| A、3 | B、2 | C、1 | D、0 |