题目内容
15.某几何体的三视图如图,其正视图中的曲线部分为半圆,则该几何体的表面积为( )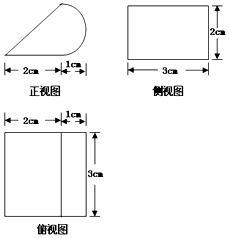
| A. | (19+π)cm2 | B. | (22+4π)cm2 | C. | (10+6$\sqrt{2}$+4π)cm2 | D. | (13+6$\sqrt{2}$+4π)cm2 |
分析 由已知中的三视图,可得该几何体是一个以俯视图为底面的柱体,代入柱体表面积公式,可得答案.
解答 解:由已知中的三视图,可得该几何体是一个以俯视图为底面的柱体,
(也可以看成是一个三棱柱与半圆柱的组合体),
其底面面积S=$\frac{1}{2}$×2×2+$\frac{1}{2}$π=(2+$\frac{1}{2}$π)cm2,
底面周长C=2+$\sqrt{{2}^{2}+{2}^{2}}$+$\frac{1}{2}•2π$=(2+2$\sqrt{2}$+π)cm,
柱体的高为3cm,
故几何体的表面积S=2×(2+$\frac{1}{2}$π)+(2+2$\sqrt{2}$+π)×3=(10+6$\sqrt{2}$+4π)cm2,
故选:C.
点评 本题考查的知识点是柱体的体积和表面积公式,简单几何体的三视图,难度中档.

练习册系列答案
相关题目
5.函数f(x)=$\frac{A}{sin(ωx+φ)}(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,则$f(\frac{3π}{2})$=( )
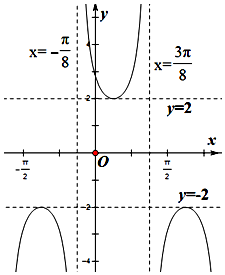

| A. | $2\sqrt{3}$ | B. | $-2\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $-2\sqrt{2}$ |
6.一个几何体的三视图如图所示,则这个几何体的表面积为( )
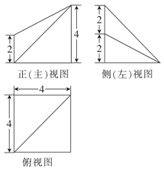

| A. | 40+8$\sqrt{2}$+4$\sqrt{6}$ | B. | 40+8$\sqrt{3}$+4$\sqrt{6}$ | C. | 48+8$\sqrt{3}$ | D. | 48+8$\sqrt{2}$ |
3.若集合A={x|-4<x<3},B={x|x<cos5π},则A∩B等于( )
| A. | (-4,0) | B. | (-4,-1) | C. | (-4,1) | D. | (-3,-1) |
20.$\int_0^1{({\sqrt{2x-{x^2}}-x})dx}$等于( )
| A. | $\frac{π-2}{4}$ | B. | $\frac{π-2}{2}$ | C. | $\frac{π-1}{2}$ | D. | $\frac{π-1}{4}$ |
5.等比数列{an}中,若a4a5=1,a8a9=16,则公比q等于( )
| A. | $\sqrt{2}$ | B. | 2 | C. | -2 | D. | $±\sqrt{2}$ |