题目内容
16.已知圆F方程为(x-1)2+y2=1,圆外一点P到圆心的距离等于它到y轴距离,(1)求点P的轨迹方程.
(2)直线l与点P轨迹方程交于y轴的右侧A,B不同两点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=-4(O为坐标原点),且4$\sqrt{6}$≤|$\overrightarrow{AB}$|≤4$\sqrt{30}$,求直线l的斜率k的取值范围.
分析 (1)由题意可知$\sqrt{(x-1)^{2}+{y}^{2}}$-1=丨x丨,整理得:y2=2x+丨x丨,去掉绝对值,即可求得点P的轨迹方程;
(2)设直线方程,代入椭圆方程,利用韦达定理及向量的数量积的坐标运算,求得m和k的关系,由△>0,求得k的取值范围,利用弦长公式,解一元二次不等式,即可求得k的取值范围.
解答 解:(1)设P(x,y) 则$\sqrt{(x-1)^{2}+{y}^{2}}$-1=丨x丨,则y2=2x+丨x丨,
∴P点的轨迹方程为:当x≥0时,y2=4x,
当x<0时,y=0,
∴点P的轨迹方程$\left\{\begin{array}{l}{{y}^{2}=4x}&{x≥0}\\{y=0}&{x<0}\end{array}\right.$;
(2)设 l:y=kx+m显然 k≠0 设A(x1,y1),B(x2,y2),
则$\left\{\begin{array}{l}{y=kx+m}\\{{y}^{2}=4x}\end{array}\right.$,整理得k2x2+(2km-4)x+m2=0,(其中k≠0),
则x1+x2=$\frac{4-2km}{{k}^{2}}$,x1x2=$\frac{{m}^{2}}{{k}^{2}}$,
由$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=-4,则 m=-2k,
代入△=(2km-4)2-4k2m2>0,解得:km<0,则-2k2<1成立,
丨AB丨=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$,
=$\frac{4}{{k}^{2}}$$\sqrt{(1+{k}^{2})^{2}(1+2{k}^{2})}$,
由4$\sqrt{6}$≤|$\overrightarrow{AB}$|≤4$\sqrt{30}$,则4$\sqrt{6}$≤$\frac{4}{{k}^{2}}$•$\sqrt{(1+{k}^{2})^{2}(1+2{k}^{2})}$≤4$\sqrt{30}$,
6≤$\frac{(1+{k}^{2})(1+2{k}^{2})}{{k}^{4}}$≤30,
即$\left\{\begin{array}{l}{4{k}^{4}-3{k}^{2}-1≤0}\\{28{k}^{4}-3{k}^{2}-1≥0}\end{array}\right.$,解得:$\frac{1}{4}$≤k2≤1,
∴$\frac{1}{2}$≤k≤1,或-1≤k≤-$\frac{1}{2}$.
∴直线l的斜率k的取值范围[-1,-$\frac{1}{2}$]∪[$\frac{1}{2}$,1].
点评 本题考查直线与抛物线的位置关系,考查韦达定理,弦长公式及一元二次不等式的解法,考查计算能力,属于中档题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |

| A. | $\frac{3}{2}$ | B. | $\frac{{\sqrt{6}}}{4}$ | C. | $\frac{5}{2}$ | D. | 4 |
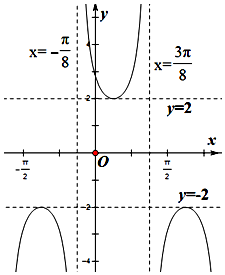
| A. | $2\sqrt{3}$ | B. | $-2\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $-2\sqrt{2}$ |
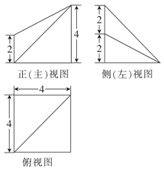
| A. | 40+8$\sqrt{2}$+4$\sqrt{6}$ | B. | 40+8$\sqrt{3}$+4$\sqrt{6}$ | C. | 48+8$\sqrt{3}$ | D. | 48+8$\sqrt{2}$ |
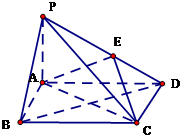 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.